Main

Schwingungen und Wellen, Akustik

Schwingungen

Allgemein

Schwingungen entstehen, wenn eine rücktreibende Kraft vorhanden ist. Bei aperiodischen Schwingungen wiederholt sich der Vorgang nicht. Bei periodischen Schwingungen hingegen schon. Beschrieben werden diese mit der Zeit \(T\) zwischen zwei Wiederholungen und der Anzahl Schwingungen pro Sekund bzw. Frequenz \(f\):

\[f=\frac{1}{T}\]

Bei echt periodischen Schwingungen bleibt die maximale Auslenkung also Amplitude konstant, es geht keine Energie verloren und man spricht von ungedämpften Schwingungen. Falls die Auslenkung mit Hilfe von \(\sin\) und \(\cos\) beschrieben werden kann, die rücktreibende Kraft proportional zur Auslenkung ist, spricht man von harmonischen Schwingungen

Mathematische Beschreibung

Allgemein

Schwingungen lassen sich als Kreisbewegungen projizieren. Es gibt also eine Winkelgeschwindigkeit \(\omega=2\pi\cdot f\) des Winkels \(\varphi\) und der Radius entspricht der Amplitude \(x_0\):

\[\begin{align} x(t)&=x_0\cdot\sin(\omega\cdot t)\\[11pt] v_x(t)=x'(t)&=x_0\cdot\omega\cdot\sin(\omega\cdot t)&&(\textrm{Geschwindigkeitsamplitude:}\,x_0\cdot\omega)\\[11pt] a_x(t)=x''(t)&=-x_0\cdot\omega^2\cdot\sin(\omega\cdot t)=-\omega^2\cdot x(t)&&(\textrm{Beschleunigungsamplitude:}\,x_0\cdot\omega^2)\\[11pt] F_{\textrm{res}}&=-m\cdot\omega^2\cdot x(t) \end{align}\]

Das Fadenpendel

Für die Position \(x(t)\) auf der Kreislinie mit Länge \(l\) des Fadens gilt:

\[x(t)=\varphi(t)\cdot l\]

mit

\[\varphi(t)=\varphi_0\cdot\sin(\omega\cdot t)\]

Geschwindigkeit und Beschleunigung können dementsprechend berechnet werden. Nehmen wir jetzt als rücktreibende Kraft die Gravitation ergibt sich:

\[\begin{align} -G\cdot\sin(\varphi(t))&=m\cdot a_x(t)\\[11pt] -m\cdot g\cdot\sin(\varphi(t))&=m\cdot l\cdot \varphi''(t)\\[11pt] \varphi''(t)&=\frac{g}{l}\cdot\sin(\varphi(t))\\[11pt] \varphi''(t)&\approx\frac{g}{l}\cdot\varphi(t) \end{align}\]

Für die Winkelgeschwindigkeit \(\omega\) eines Fadenpendels gilt für kleine Winkel (\(\sin(\varphi(t)))\approx\varphi(t)\):

\[\omega=\sqrt{\frac{g}{l}}\]

Das Federpendel

Beim Federpendel ist die Federkraft die rücktreibende Kraft:

\[\begin{align} -D\cdot x(t)&=m\cdot a_x(t)\\[11pt] x''(t)&=-\frac{D}{m}\cdot x(t) \end{align}\]

Für die Winkelgeschwindigkeit \(\omega\) eines Federpendels gilt:

\[\omega=\sqrt{\frac{D}{m}}\]

Resonanz

Die Amplitude bleibt aufgrund von Energieverlusten normalerweise nicht konstant, sondern sie wird abgedämpft. Will man, dass sie das bleibt, muss periodisch Energie hinzugefügt werden (Z. B. Anstossen Schaukel). Die Amplitude bleibt also konstant, weil die Energiezufuhr dem Energieverlust entspricht. Sie hängt von der Anregungsfrequenz und der Eigenfrequenz ab und ist am grössten, wenn diese übereinstimmen. Man spricht dann von Resonanz.

Wellen

Allgemein

Wellen sind Störungen / Auslenkungen \(U\), die sich in einem Medium fortpflanzen. Dafür müssen "Pendel" mit Kopplungen dazwischen vorhanden sein. Es werden Energie, Impuls und Information transportiert.

Zum Zeichnen werden Ortsbilder (Zeit ist fest) und Zeitbilder (Ort ist fest) verwendet.

Harmonische Wellen

Harmonische Wellen sind im Grunde Wellen mit harmonisch schwingenden Pendeln. Für die Geschwindigkeit \(v_W\) eine Welle mit Wellenlänge \(\lambda\) und Schwingungsdauer \(T\) / Frequenz \(f\) gilt:

\[v_W=\frac{\lambda}{T}=\lambda\cdot f\]

Überlagerung und Interferenz

Superpositionsprinzip

Wenn Wellen aufeinander treffen, so addieren sich ihre Auslenkungen inklusive Vorzeichen.

Schwebungen

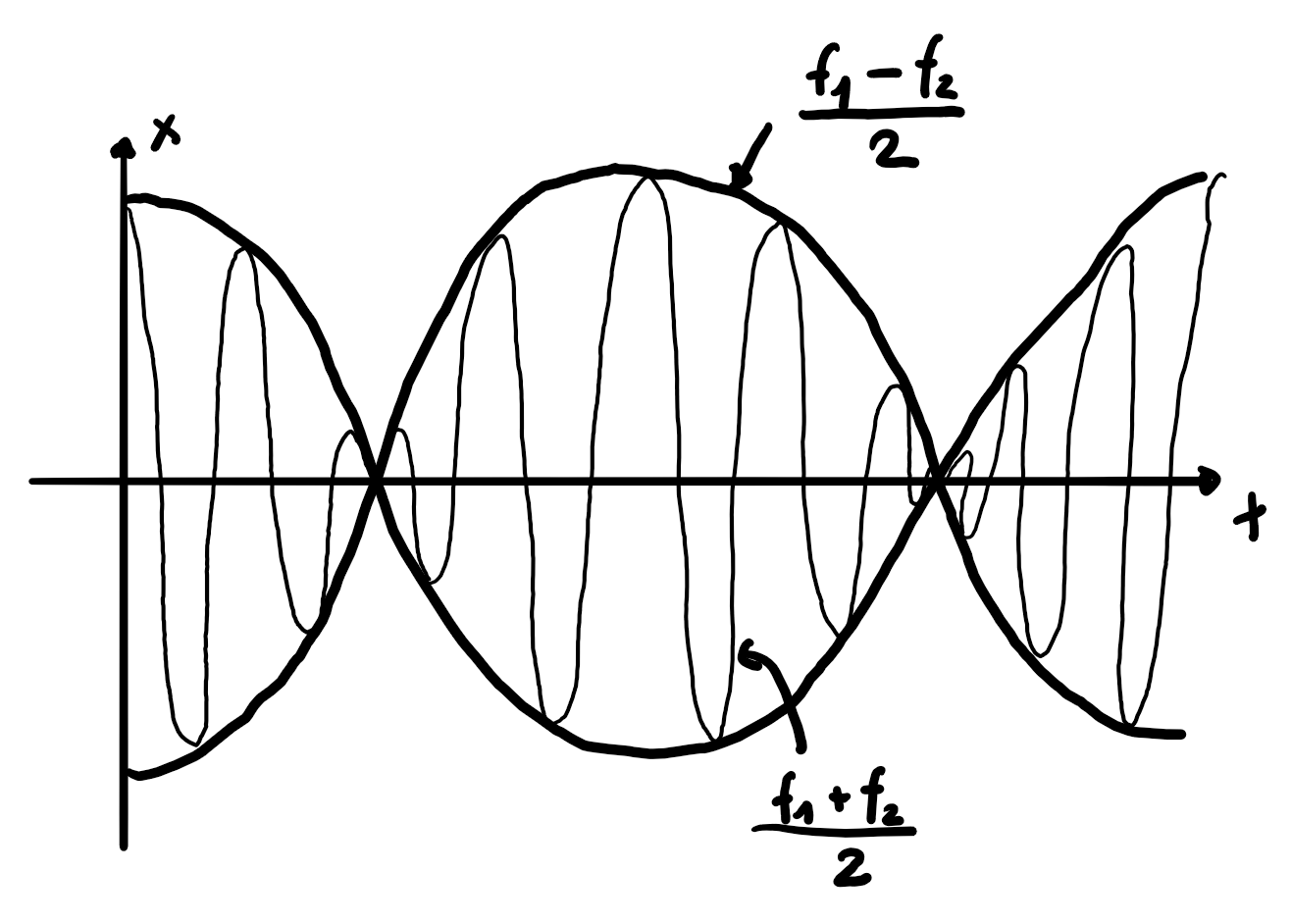
Schwebungen sind Überlagerung von zwei Schwingungen mit unterschiedlichen Frequenzen \(f_1\) und \(f_2\). Es entsteht eine schnelle Schwingung mit \(\frac{f_1+f_2}{2}\) mit einer zeitabhängige Amplitude \(\frac{f_1-f_2}{2}\).

Interferenz

Wenn zwei Wellen mit gleichem \(\lambda\) aufeinandertreffen und um \(n\cdot\lambda\) (Verstärkung) bzw. um \((n+\frac{1}{2})\cdot\lambda\) (Auslöschung) verschoben sind, dann spricht man von Interferenz. Zusätzlich müssen die Zeitabstände konstant bleiben.

Überlagerung von 2 Wellen

Bei der Überlagerung von zwei Wellen mit punktförmigen Quellen entstehen Interferenzmuster.

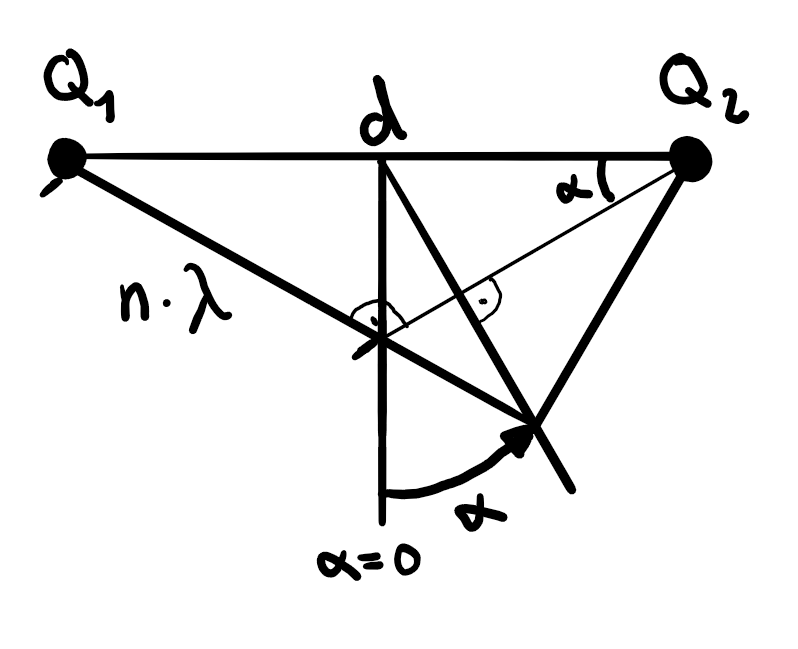
Für die Winkel der Maxima \(\alpha_{\textrm{max}}\) gilt:

\[\sin(\alpha_{\textrm{max}})=\frac{n\cdot\lambda}{d}\]

Bei Gittern mit \(N\) Spalten ist die totale Intensität proportional zu \(N^2\).

Doppelspalt

Wenn Licht / Wasser auf einen Doppelspalt trifft, entsteht folgendes Interferenzmuster:

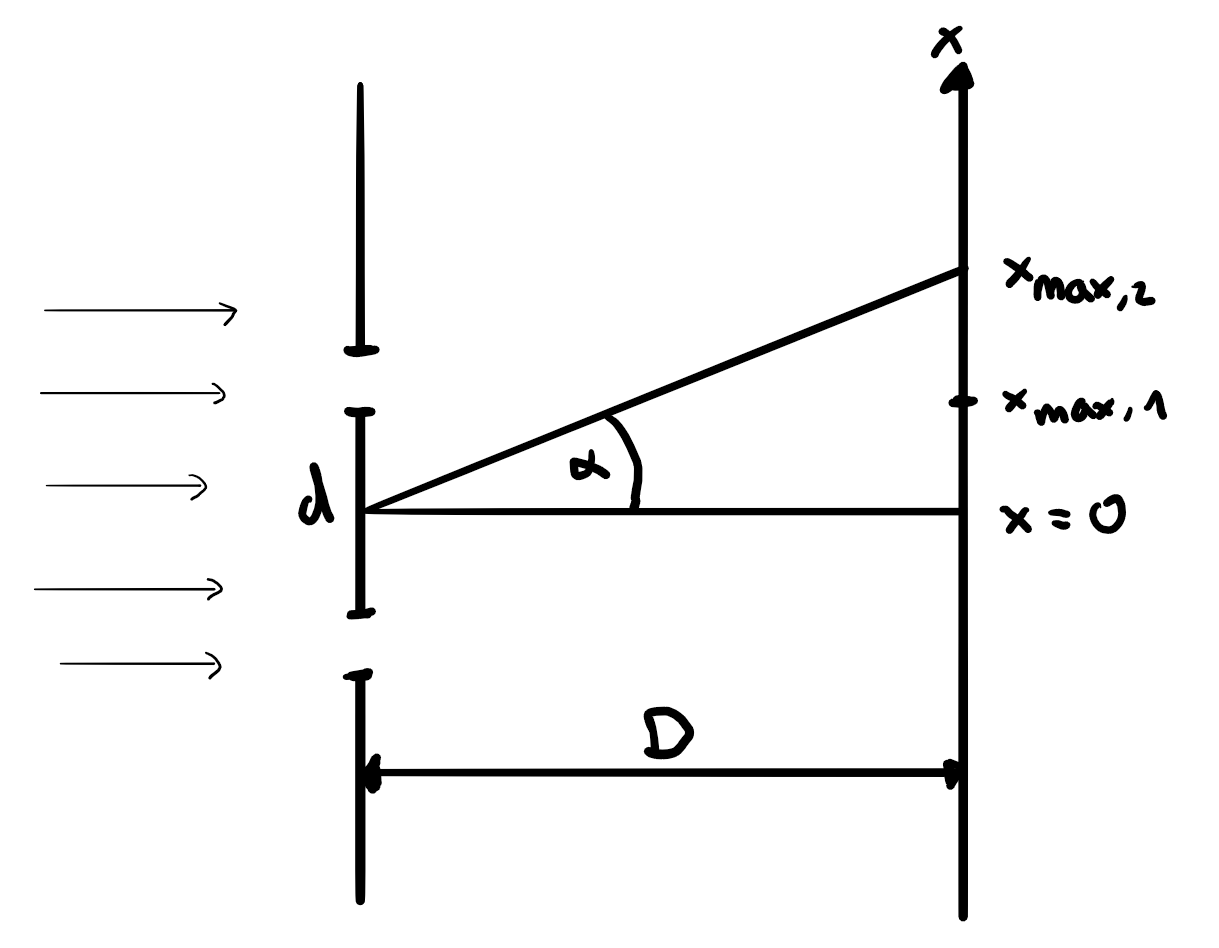
Für die Positionen an der Wand der Maxima gilt:

\[x_{\textrm{max}}=D\cdot\tan(\alpha_{\textrm{max}})\approx D\cdot\sin(\alpha_{\textrm{max}})\]

Daraus folgen:

\[\begin{align} x_{\textrm{max}}&\approx D\cdot n\cdot\frac{\lambda}{d}\\[11pt] \Delta x_{\textrm{max}}&\approx D\cdot\frac{\lambda}{d} \end{align}\]

Beugung am Einzelspalt

Für die Winkel der Minima \(\alpha_{\textrm{min}}\) gilt eines Einzelspaltes mit Breite \(s\):

\[\sin(\alpha_{\textrm{min}})=\frac{n\cdot\lambda}{s}\;(n\not=0)\]

Farben dünner Schichten

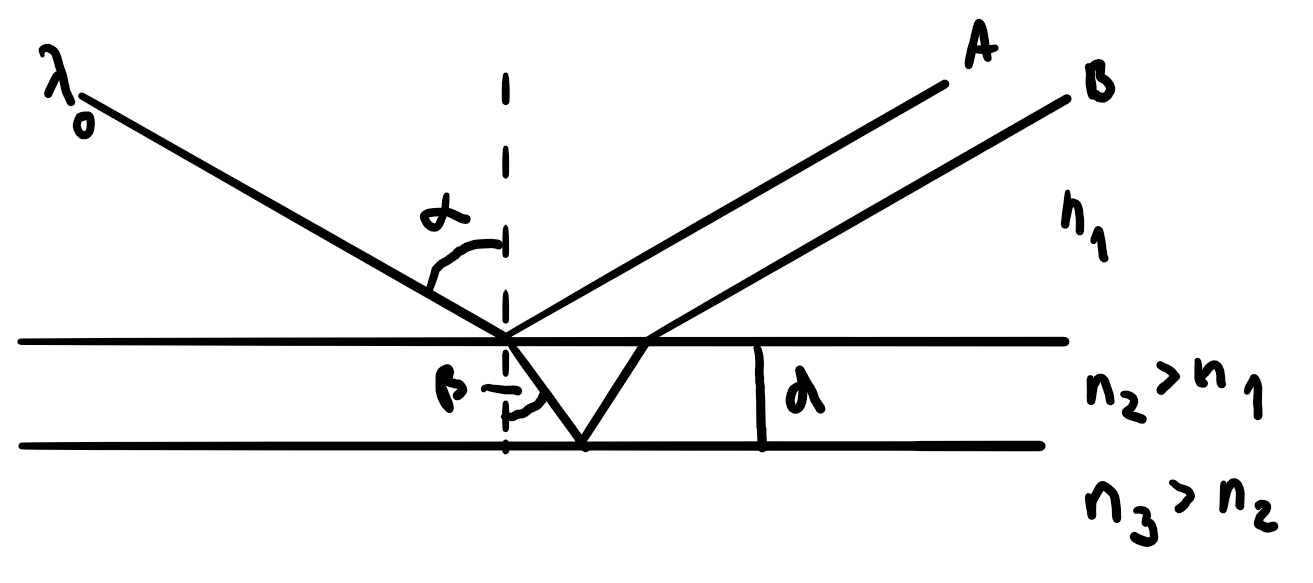
Auch hier entstehen Interferenzmuster, aufgrund der Verschiebung durch die Reflexionen.

Es gilt (ohne Herleitung):

\[\begin{align} m\cdot\frac{\lambda_0}{n_2}&=\frac{2d}{\sqrt{1-\left(\sin(\alpha)\cdot\frac{n_1}{n_2}\right)^2}}\;\textrm{(Verstärkung)}\\[11pt] \left(m+\frac{1}{2}\right)\cdot\frac{\lambda_0}{n_2}&=\frac{2d}{\sqrt{1-\left(\sin(\alpha)\cdot\frac{n_1}{n_2}\right)^2}}\;\textrm{(Auslöschung)} \end{align}\]

Um die Reflexion zu Vermindern, werden Glasoberflächen vergütet. Spezialfall, wenn \(n_1=1\) (Luft), \(\alpha=0\) (senkrechter Lichteinfall) und \(m=0\):

\[d=\frac{\lambda_0}{4n_2}\]

Das Huygenssche Prinzip

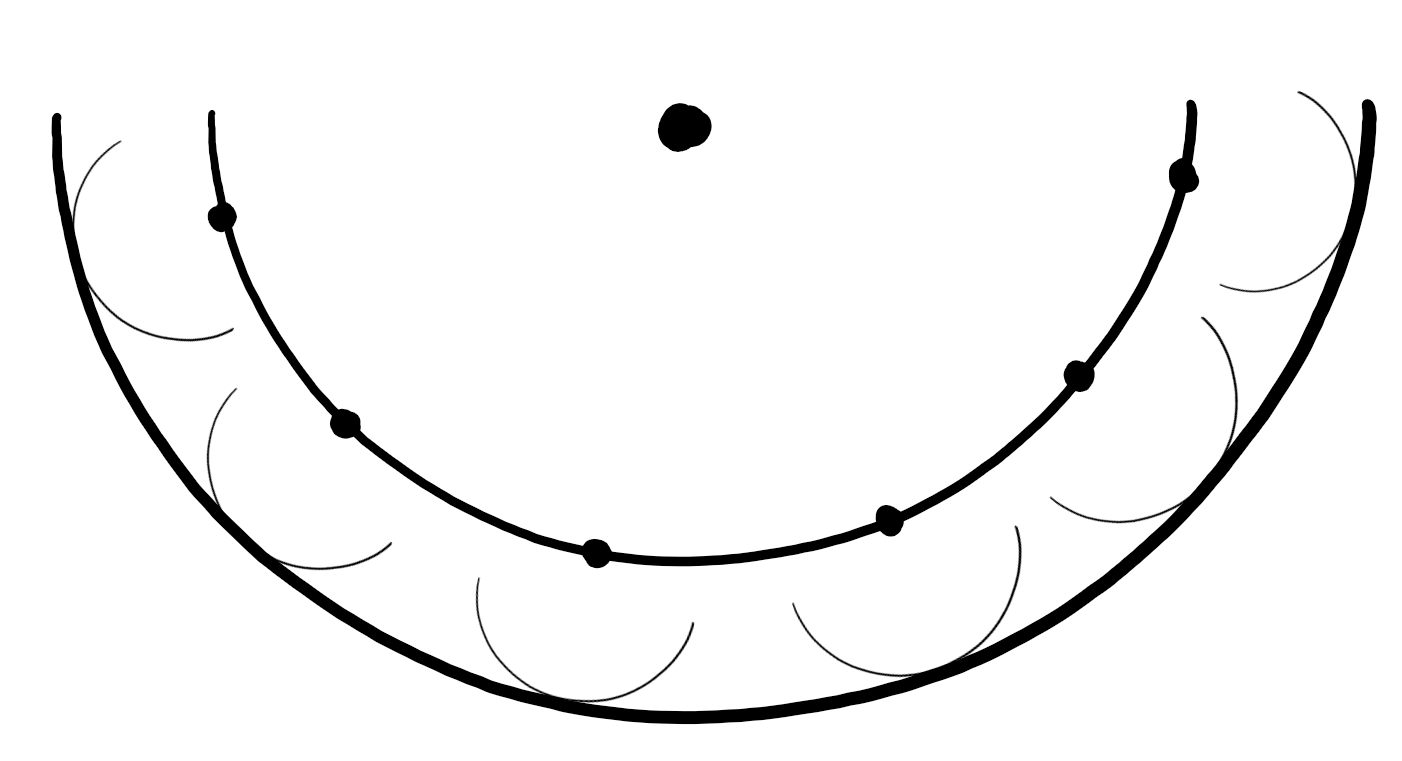
Jeder Punkt einer Wellenfront (Punkte mit gleicher Schwingungsphase) ist Ausgangspunkt (Punktquelle) einer neuen kugelförmigen Welle.

Akustik

Allgemein

Die Akustik untersucht die Entstehungen, die Ausbreitung und die Eigenschaften des Schalls. Schallwellen sind mechanische Schwingungen, die sich in einem Medium ausbreiten. Es entstehen Dichte- bzw. Druckschwankungen.

Lochsirene

Bläst man auf einem "Lochkreis", so wird der Luftstrom in regelmässigen Zeitabständen unterbrochen. Es entstehen periodische Druckschwankungen. Für die Frequenz \(f\) einer Lochsirene mit \(n\) Löchern und die Anzahl \(U\) der Umdrehungen pro Sekunde gilt:

\[f=n\cdot U\]

Saiten

Für die Geschwindigkeit \(v\) einer Saite mit Zugkraft \(F\), Masse \(m\), Länge \(l\), Dichte \(\rho\) und Querschnittsfläche \(A\) gilt:

\[v=\sqrt{\frac{F}{m}\cdot l}=\sqrt{\frac{F\cdot l}{V\cdot\rho}}=\sqrt{\frac{F}{A\cdot\rho}}\]

Natürlich gilt auch hier \(v_W=\lambda\cdot f\).

An den Enden einer Seite ist die Auslenkung 0, da sie dort festgemacht sind (Reflexion). Es entsteht also stehende Wellen aus der Überlagerung von 2 gegeneinanderlaufenden Wellen mit gleichem \(\lambda\).

Für die Grundschwingung \(n=0\) mit \(f_0=\frac{v}{2L}\) und die Oberschwingungen \(n>0\) einer Saite mit Länge \(L\) gelten:

\[\begin{align} \lambda_n&=\frac{2L}{n+1}\\[11pt] f_n&=(n+1)\cdot f_0 \end{align}\]

Röhren / Pfeifen

Röhren können beidseitig offen oder einseitig geschlossen sein. In beiden Fällen kommt es auf Grund von Druckunterschieden zu den verschiedenen Schwingungen. An den offenen Enden beider Röhrentypen ist der Druckunterschied \(\Delta p=0\) und die Auslenkung ist am grössten \(|u_{\textrm{max}}|\). An der geschlossenen Seite ist der Druckunterschied am grössten \(|p_{\textrm{max}}|\) und für die Auslenkung gilt \(\Delta u=0\).

Für die Geschwindigkeit \(v\) einer Röhre mit der universellen Gaskonstante \(R\), der Temperatur \(T\), der Molmasse \(M\) in kg und der Konstante \(K\) mit \(\begin{cases}\frac{5}{3} &\textrm{Für 1-atom. Gase}\\\frac{7}{5} &\textrm{Für 2-atom. Gase}\end{cases}\) gilt:

\[v=\sqrt{\frac{R\cdot T\cdot K}{M}}\]

Für die Grundschwingung \(n=0\) mit \(f_0=\frac{v}{2L}\) und die Oberschwingungen \(n>0\) einer beidseitig offenen Pfeife mit Länge \(L\) gelten:

\[\begin{align} \lambda_n&=\frac{2L}{n+1}\\[11pt] f_n&=(n+1)\cdot f_0 \end{align}\]

Sie sind also äquivalent zu Saiten.

Für die Grundschwingung \(n=0\) mit \(f_0=\frac{v}{4L}\) (1 Oktave tiefer als bei beidseitig offen) und die Oberschwingungen \(n>0\) einer einseitig geschlossenen Pfeife mit Länge \(L\) gelten:

\[\begin{align} \lambda_n&=\frac{4L}{2n+1}\\[11pt] f_n&=(2n+1)\cdot f_0 \end{align}\]

Lautstärke

Der Schallpegel \(L\) wird mit der Intensität \(I=\frac{\textrm{Energie}}{\textrm{Zeit}\cdot\textrm{Fläche}}\) und der Hörgrenze \(I_0=10^{-12}\;W/m^2\) in dB definiert:

\[L=10\cdot\log_{10}\left(\frac{I}{I_0}\right)\]

Auch hier ist die Energie proportional zur Auslenkung (in diesem Fall die Druckschwankung \(\Delta p\)) im Quadrat \(I\sim(\Delta p)^2\). Man also schreiben:

\[L=20\cdot\log_{10}\left(\frac{\Delta p}{\Delta p_{\textrm{min}}}\right)\]

Für verschiedene Quellen mit Abständen \(r\) gilt:

\[\begin{align} &\textrm{Punktquelle}:&&I\sim\frac{1}{r^2}\\[11pt] &\textrm{Lange Gerade als Quelle}:&&I\sim\frac{1}{r}\\[11pt] &\textrm{Grosse Fläche als Quelle}:&&I\;\textrm{nimmt nicht mit Abstand ab} \end{align}\]

Doppler-Effekt

Bewegen sich Quelle und/oder Person, dann ändert sich auch die Frequenz des Tones. Es gilt:

\[\begin{align} \textrm{Quelle bewegt sich zur Person}:&&f'=\frac{c}{c-v}\cdot f\\[11pt] \textrm{Quelle bewegt sich von Person weg}:&&f'=\frac{c}{c+v}\cdot f\\[11pt] \textrm{Person bewegt sich zur Quelle}:&&f'=\frac{c+v}{c}\cdot f\\[11pt] \textrm{Person bewegt sich von Quelle weg}:&&f'=\frac{c-v}{c}\cdot f\\[11pt] \end{align}\]

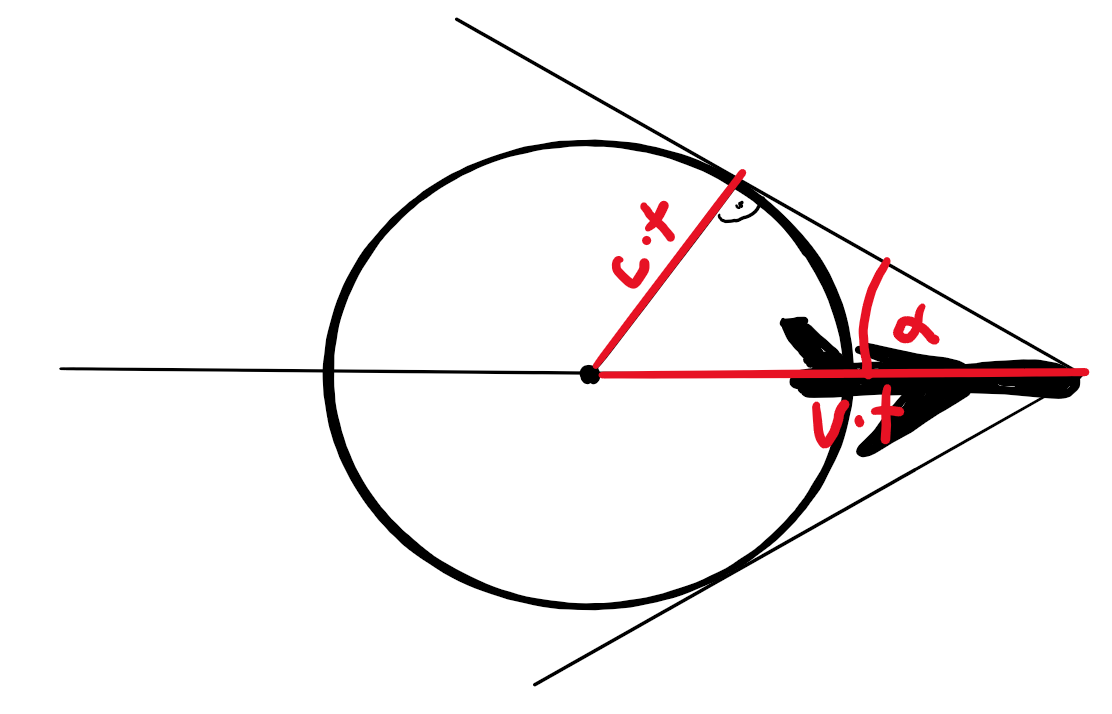
Für den Machkegel gilt:

\[\sin(\alpha)=\frac{c}{v}\]

---

Last update: May 30, 2021