Main

Die Ebene im Raum

Parameterform und Koordinatengleichung

Parameterform

Jeder Punkt in einer Ebene kann durch eine Kombination eines Ortsvektor \(\vec{p}\) (Vektor zu einem bekannten Punkt in der Ebene) und zweier Richtungsvektoren \(\vec{u}\) und \(\vec{v}\) beschrieben werden:

\[\begin{align} \vec{OP}&=\vec{p}+s\vec{u} +t\vec{v}\\[11pt] \left(\begin{array}{c}P_x\\P_y\\P_z \end{array}\right)&=\left(\begin{array}{c}p_x\\p_y\\p_z \end{array}\right) + s\left(\begin{array}{c}u_x\\u_y\\u_z \end{array}\right) + t\left(\begin{array}{c}v_x\\v_y\\v_z \end{array}\right) \end{align}\]

Koordinatengleichung

Jeder Punkt in einer Ebene steht senkrecht zum Normalenvektor \(\vec{n}\) der Ebene und kann somit durch diesen und einem Ortsvektor \(\vec{p}\) beschrieben werden.

\[\begin{align} \left(\begin{array}{c}x-p_x\\y-p_x\\z-p_x \end{array}\right)\cdot \left(\begin{array}{c}n_x\\n_y\\n_z \end{array}\right) &= 0 \\[11pt] n_xx+n_yy+n_zz &= n_xp_x + n_yp_y + n_zp_z\\[11pt] Ax+By+Cz &= D \end{align}\]

Parallele Ebenen besitzen also kollineare Normalenvektoren.

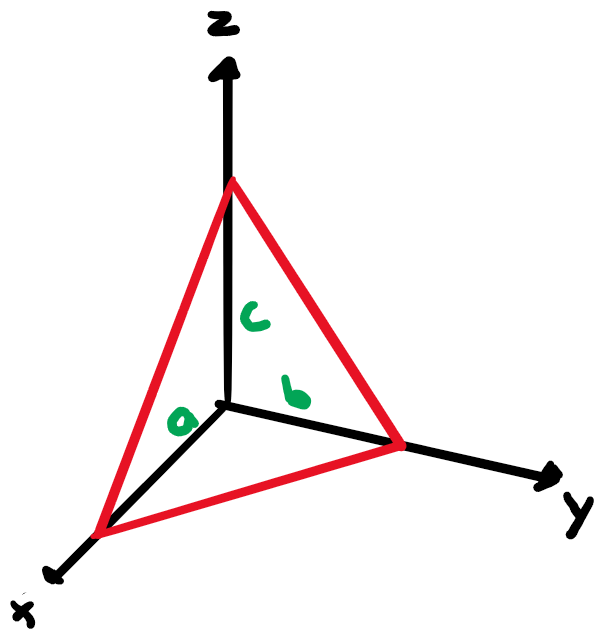
Das Spurendreieck (Dreieck aus den Schnittpunkten mit den Achsen) kann mit Achsenabschnittsgleichung bestimmt werden:

\[\begin{align} Ax+By+Cz &= D\\[11pt] \frac{x}{D/A} + \frac{y}{D/B} + \frac{z}{D/C} &=1\\[11pt] \frac{x}{a} + \frac{y}{b} + \frac{z}{c} &= 1 \end{align}\]

Spezielle Ebenen

Ebene geht durch den Origo

\[Ax+By+Cz = 0\]

Ebene ist parallel zur z-Achse

\[Ax+By+0z = D\]

Ebene ist parallel zur xz-Ebene

\[0x+By+0z = D\]

Normalebene und Mittelnormalebene

Die Normalebene steht senkrecht zu einer Geraden. Der Richtungsvektor der Geraden ist somit der Normalenvektor der Ebene.

Auf der Mittelnormalebene liegen alle Punkte \(P\) mit gleichem Abstand zu \(A\) und \(B\). Koordinatengleichung mit Normalenvektor \(\vec{AB}\) und Mittelpunkt \(M\).

Krumme Flächen

Krumme Flächen haben nicht-lineare Beziehungen zwischen \(x\), \(y\), und \(z\). Bsp.:

\[xy + 3y^2 + 5z = 10\]

Lösungsideen

Von der Parameterform zur Koordinatengleichung

1. Normalenvektor durch das Kreuzprodukt beider Richtungsvektoren bestimmen (steht ja senkrecht) und diesen gegebenenfalls "kürzen"
2. Ortsvektor in \(Ax+By+Cz = D\) einsetzen (\(A\), \(B\) und \(C\) sind schon aus \(\vec{n} = \left(\begin{array}{c}A\\B\\C \end{array}\right)\) gegeben) und ausrechnen.

Koordinatengleichung aus 3 Punkten

1. Richtungsvektoren aus den 3 Punkten.
2. Wie in der vorherigen Lösung vorgehen.

Schnittpunkt der Ebene E und der Geraden g

1. In der Koordinatengleichung von \(E\) für \(x\), \(y\) und \(z\) die Parameterform von \(g\) einsetzen
2. Das so erhaltene \(t\) für die Parameterform wieder einsetzen und Punkt berechnen

Abstand d vom Punkt P zur Ebene E

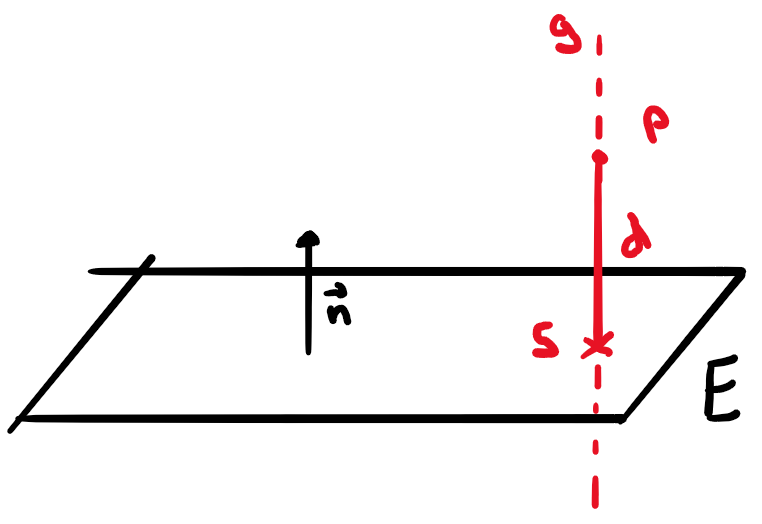
1. Gerade \(g\) durch \(P\) mir Richtungsvektor gleich dem Normalenvektor \(\vec{n}\) der Ebene.
2. Schnittpunkt \(S\) von \(g\) mit \(E\) (Lösung Beispiel vorher)
3. \(d=|\vec{PS}|\)

Koordinatengleichung der Ebene E parallel zur Ebenen F mit Abstand d

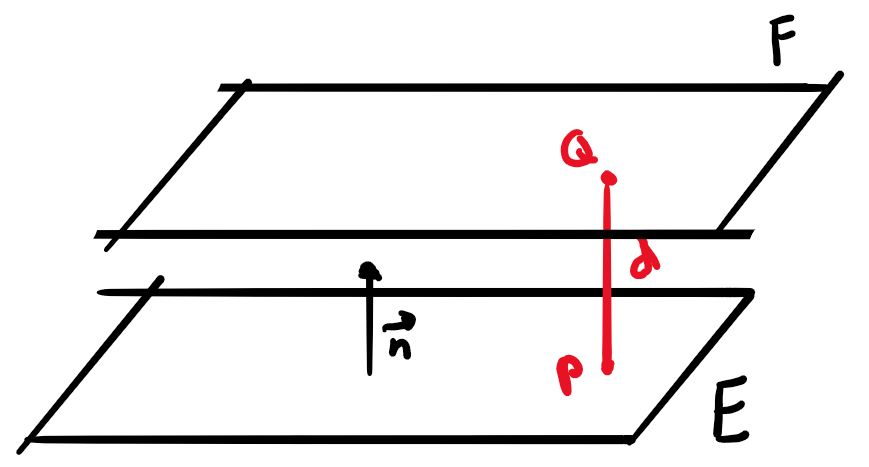
1. Punkt \(P\) auf der Ebene \(E\) finden mit einem willkürlichen Punkt \(Q\) auf \(F\). \(\vec{OP} = \vec{OQ} \pm \lambda\vec{n}\) mit \(\lambda|\vec{n}| = d\) ("\(\pm\)", weil es auf beiden Seiten Lösungen hat)
2. Koordinatengleichung für \(E\) benutzt das gleiche \(\vec{n}\) und man setzt \(P\) ein, um \(D\) zu berechnen.

Punkt P an Ebene E spiegeln

1. Abstandsvektor \(d\) zwischen \(P\) und \(E\)
2. \(\vec{OP'} = \vec{OS} + \vec{PS} = \vec{OP} + 2\vec{PS}\)

Lichtstrahl l an der Ebene E reflektieren

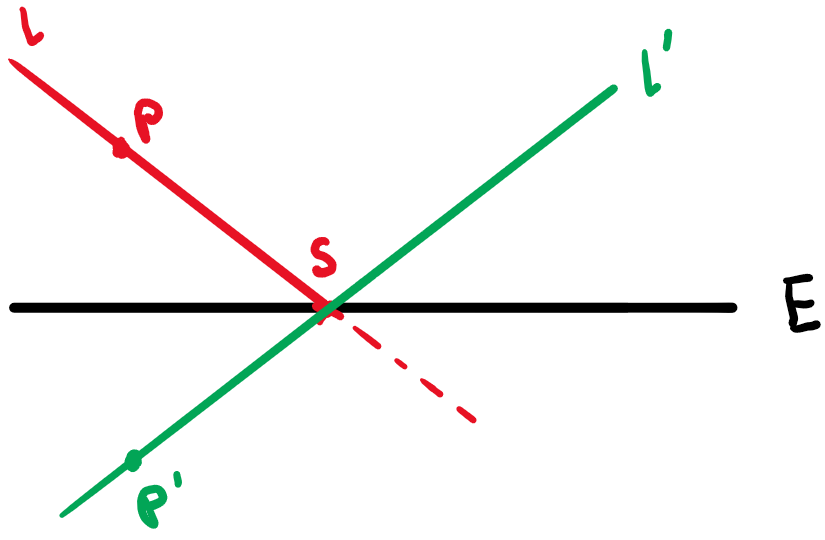
1. Punkt \(P\) aus der Parameterform der Geraden \(l\) an \(E\) spiegeln (siehe vorheriges Beispiel)
2. Schnittpunkt \(S\) der Geraden \(l\) und Ebenen \(E\)
3. Parameterform mit \(P'\) und \(\vec{P'S}\)

Winkel zwischen 2 Ebenen E und F

1. Schnittwinkel zwischen den beiden Normalenvektoren bestimmen.

Winkel zwischen der Geraden g und der Ebene E

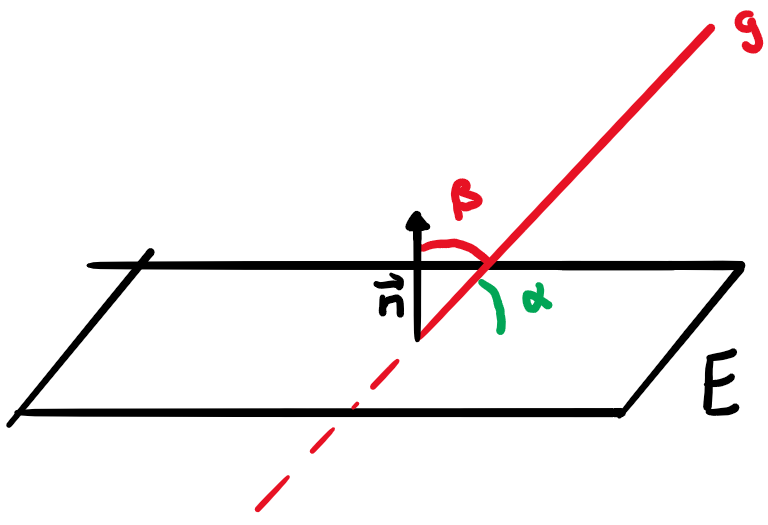
1. \(\beta\) ist der Winkel zwischen \(g\) bzw. dessen Richtungsvektor und dem Normalenvektor \(\vec{n}\)
2. \(\alpha = 90° - \beta\)
3. Wenn \(\beta>90°\), dann \(\alpha = 180° - \beta\)

Abstand d vom Punkt P zur Geraden g (mit Normalebene)

1. Normalebene \(N\) zu \(g\) durch \(P\)
2. \(N\) mit \(g\) schneiden ergibt \(D\)
3. \(d = |\vec{DP}|\)

---

Last update: June 7, 2021