Skalar-, Vektor- und Spatprodukt

Skalarprodukt

Neue Formel

Aus dem Kosinussatz:

\[\begin{align} |\vec{a}-\vec{b}|^2&=|\vec{a}|^2 + |\vec{b}|^2 - 2|\vec{a}||\vec{b}|\cos(\alpha)=|\vec{a}|^2 + |\vec{b}|^2 - \vec{a}\cdot\vec{b} \\[11pt] \vec{a}\cdot\vec{b} &= \frac{|\vec{a}|^2 + |\vec{b}|^2 - |\vec{a}-\vec{b}|^2}{2}\\[11pt] &=...\\[11pt] &=a_1b_1+a_2b_2+a_3b_3 \end{align}\]

Winkel zwischen zwei Vektoren

\[\begin{align} \vec{a}\cdot\vec{b} &= |\vec{a}||\vec{b}|\cos(\alpha)\\[11pt] \cos(\alpha) &= \frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|} \end{align}\]

Wobei das Skalarprodukt nun mit den aus dem Kosinussatz hergeleiteten Komponenten berechnet werden kann.

\[\cos(\alpha) = \frac{a_1b_1+a_2b_2+a_3b_3}{|\vec{a}||\vec{b}|}\]

Vektor-/Kreuzprodukt

Idee

"Schöner" Vektor \(\vec{n}\) der sowohl zu \(\vec{a}\) als auch zum Vektor \(\vec{b}\) senkrecht steht.

Folgende Bedingungen müssen erfüllt sein:

\[\vec{n}\cdot\vec{a} = 0\]
\[\vec{n}\cdot\vec{b} = 0\]
\[n_1a_1+n_2a_2+n_3a_3 = 0\]
\[n_1b_1+n_2b_2+n_3b_3 = 0\]

Man kann nun 3. nach \(n_1\) auflösen und erhält:

\[n_1=\frac{-n_2a_2-n_3a_3}{a_1}\]

Durch einsetzen von 3. in 4. erhält man nach auflösen:

\[n_2(a_1b_2-a_2b_1) + n_3(a_1b_3-a_3b_1) = 0\]

Dies lässt auf die Lösungen mit \(n_2=a_3b_1-a_1b_3\) und \(n_3=a_1b_2-a_2b_1\) führen. Schliesslich setzt man das in \(n_1\) ein und erhält für \(\vec{n}\):

\[\vec{n} = \left(\begin{array}{c}a_2b_3-a_3b_2\\a_3b_1-a_1b_3\\a_1b_2-a_2b_1 \end{array}\right) \]

Dieser Vektor ist das Ergebnis des Vektor-/Kreuzproduktes von \(\vec{a}\) und \(\vec{b}\):

\[\vec{a}\times\vec{b} = \left(\begin{array}{c}a_2b_3-a_3b_2\\a_3b_1-a_1b_3\\a_1b_2-a_2b_1 \end{array}\right) \]

Algebra-Gesetze

\[\vec{a}\times\vec{b}\neq\vec{b}\times\vec{a}\]

\[\vec{a}\times(\vec{b} + \vec{c}) = \vec{a}\times\vec{b} + \vec{a}\times\vec{c}\]

\[(\lambda\vec{a})\times\vec{b} = \lambda (\vec{a}\times\vec{b}) = \vec{a}\times(\lambda\vec{b})\]

\[(\vec{a}\times\vec{b})\times\vec{c}\neq\vec{a}\times(\vec{b}\times\vec{c})\]

Der Betrag des Vektorprodukts

\[\begin{align} |\vec{a}\times\vec{b}| &= \sqrt{(a_2b_3-a_3b_2)^2+(a_3b_1-a_1b_3)^2+(a_1b_2-a_2b_1)^2}\\[11pt] &= ... \\[11pt] &= |\vec{a}||\vec{b}|\sin(\alpha) \end{align}\]

Geometrisch ist das die Fläche des von den Vektoren \(\vec{a}\) und \(\vec{b}\) aufgespannten Parallelogramms

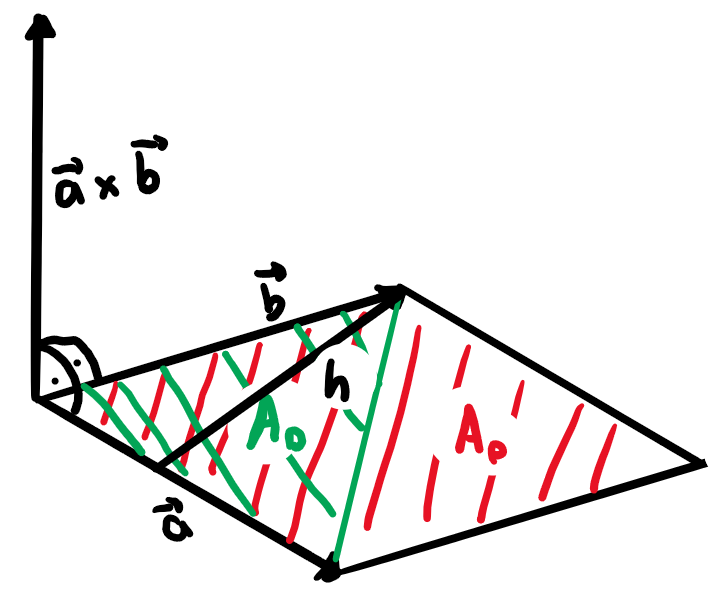
Der Betrag des Vektorprodukts

\[A_P = |\vec{a}\times\vec{b}|\]

Wobei für das Dreieck Folgendes gilt:

\[A_D = \frac{|\vec{a}\times\vec{b}|}{2}\]

Und für die Höhe \(h\):

\[h = \frac{|\vec{a}\times\vec{b}|}{|\vec{a}|}\]

Spatprodukt

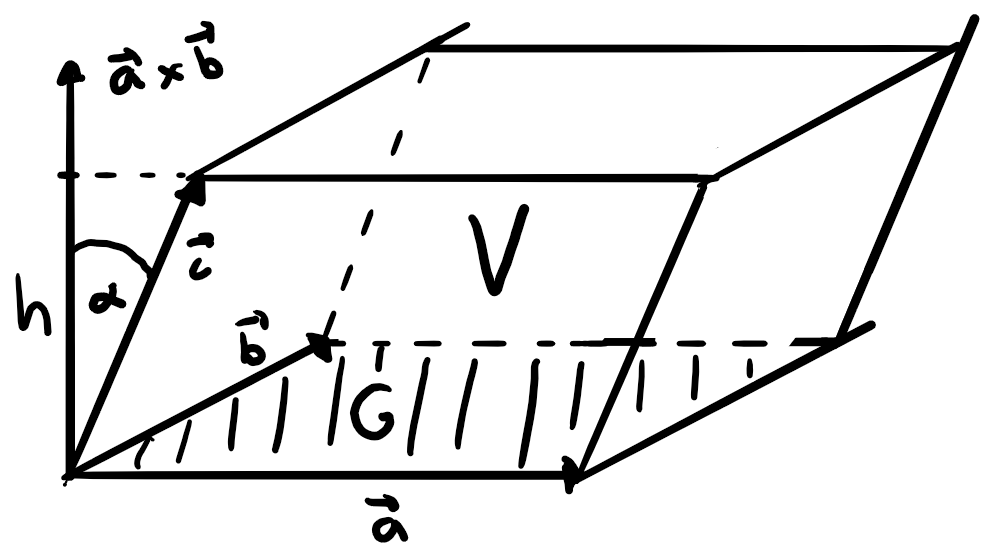
Für das Volumen \(V_S\) eines Spats gilt also:

\[\begin{align} V_S &= G\cdot h\\[11pt] &= ||\vec{a}\times\vec{b}|\cdot|\vec{c}|\cos(\alpha)|=||\vec{a}\times\vec{b}|\cdot\vec{c}| \end{align}\]

Für Rechts- und Linkssysteme (bei Linkssystemen ist das Ergebnis negativ, da das Kreuzprodukt nach oben zeigt und \(\vec{c}\) aber nach unten --> \(\cos(180^{\circ}-\alpha) = -\cos(\alpha)\)).

Wenn für das Spatprodukt \(|\vec{a}\times\vec{b}|\cdot\vec{c}=0\) gilt, befinden sich die Vektoren in der gleichen Ebene sprich sie sind komplanar. (Gl.-Systeme haben dann keine oder unendlich viele Lösungen, wenn ihr Spatprodukt 0 ist. Determinante und Spatprodukt sind dasselbe!)

Last update: June 6, 2021