Skip to content
Main

Lineare Abbildungen

Allgemein

Definition

Für eine Lineare Abbildung \(\alpha\) mit den Vektoren \(\vec{p}\) und \(\vec{q}\) gelten (Die eigentliche Definition):

\[\begin{align} \alpha(c\cdot\vec{p})&=c\cdot\alpha(\vec{p})&&\textrm{(I.)}\\[11pt] \alpha(\vec{p}+\vec{q})&=\alpha(\vec{p})+\alpha(\vec{q})&&\textrm{(II.)} \end{align}\]

Aus diesen Bedingungen folgt eine dritte Bedingung:

\[\alpha(a\cdot\vec{p}+b\cdot\vec{q})=a\cdot\alpha(\vec{p})+b\cdot\alpha(\vec{q})\;\;\textrm{(III.)}\]

Sie wird wie folgt bewiesen:

  • \(\textrm{I. + II.}\implies\textrm{III.}\;\textrm{mit}\;\vec{v}=a\cdot\vec{p}; \;\vec{u}=b\cdot\vec{q}\)
\[\begin{align} \alpha(\vec{v}+\vec{u})&\stackrel{\textrm{II.}}{=}\alpha(\vec{v})+\alpha(\vec{u})\\[11pt] &=\alpha(a\cdot\vec{p})+\alpha(b\cdot\vec{q})\\[11pt] &\stackrel{\textrm{I.}}{=}a\cdot\alpha(\vec{p})+b\cdot\alpha(\vec{q}) \end{align}\]
  • \(\textrm{III.}\implies\textrm{I.}\;\textrm{mit}\;b=0; \;a\in\mathbb{R}\)
\[\begin{align} \alpha(a\cdot\vec{p} +b\cdot\vec{q})&=a\cdot\alpha(\vec{p})+b\cdot\alpha(\vec{p})\\[11pt] &= a\cdot\alpha (\vec{p})+0\cdot\alpha(\vec{p})\\[11pt] &=a\cdot\alpha (\vec{p}) \end{align}\]
  • \(\textrm{III.}\implies\textrm{II.}\;\textrm{mit}\;a=b=1\)
\[\begin{align} \alpha(a\cdot\vec{p} +b\cdot\vec{q})&=a\cdot\alpha(\vec{p})+b\cdot\alpha(\vec{q})\\[11pt] &=\alpha(\vec{p}) +\alpha(\vec{q}) \end{align}\]

Lineare Abbildungen \(\alpha\) haben also die folgende Form:

\[\begin{align} x'&=a\cdot x + b\cdot y\\[11pt] y'&=c\cdot x + d\cdot y\\[11pt] \end{align}\]

Beweise:

  • \(\alpha\) erfüllt \(\textrm{I.}\) mit \(\vec{p}=\begin{pmatrix} p_x\\p_y\end{pmatrix}; \;\vec{q}=\begin{pmatrix} q_x\\q_y\end{pmatrix}\):
\[\begin{align} \alpha\left(\begin{pmatrix}p_x+q_x\\p_y+q_y\end{pmatrix}\right)&=\begin{pmatrix}a(p_x+q_x)+b(p_y+q_y)\\c(p_x+q_x)+d(p_y+q_y)\end{pmatrix}\\[11pt] &=\begin{pmatrix}ap_x+bp_y\\cp_x+dp_y\end{pmatrix}+\begin{pmatrix}aq_x+bq_y\\cq_x+dq_y\end{pmatrix}\\[11pt] &=\alpha(\vec{p})+\alpha(\vec{q}) \end{align}\]
  • \(\alpha\) erfüllt \(\textrm{II.}\) mit \(\vec{p}=\begin{pmatrix} p_x\\p_y\end{pmatrix}; \;\vec{q}=\begin{pmatrix} q_x\\q_y\end{pmatrix}\):
\[\begin{align} \alpha(k\cdot\vec{p})&=\alpha\left(\begin{pmatrix}kp_x\\kp_y\end{pmatrix}\right)\\[11pt] &=\begin{pmatrix} kap_x +kbp_y\\kcp_x+kdp_y \end{pmatrix}\\[11pt] &=k\begin{pmatrix}ap_x+bp_y\\cp_x+dp_y\end{pmatrix}\\[11pt] &=k\alpha(\vec{p}) \end{align}\]

Basisvektoren

Die Basisvektoren \(\vec{e_1}=\begin{pmatrix}1\\0\end{pmatrix}\) und \(\vec{e_2}=\begin{pmatrix}0\\1\end{pmatrix}\) haben die Abbildungen (So kann man \(a\), \(b\), \(c\) und \(d\) einfach bestimmen, weil man schaut, wo die Basisvektoren landen sollten):

\[\begin{align} \alpha(\vec{e_1})= \begin{pmatrix}a\\c\end{pmatrix}\\[11pt] \alpha(\vec{e_2})= \begin{pmatrix}b\\d\end{pmatrix} \end{align}\]

Fixpunkte

Für Fixpunkte gilt:

\[\begin{align} x&=a\cdot x + b\cdot y\\[11pt] y&=c\cdot x + d\cdot y \end{align}\]

Determinante

Für die Determinante \(\Delta\) gilt:

\[\Delta = a\cdot d - b\cdot c\]

Die Determinante entsteht auch beim Kreuzprodukt der abgebildeten Basisvektoren. Sie hat also folgende geometrische Bedeutungen für die Abbildung:

  1. Die Bildfigur hat eine um \(\Delta\) grössere Fläche (Beweise mit Vergleich der Dreiecksfläche der tatsächlichen Basisvektoren mit derjenigen der abgebildeten Basisvektoren)
  2. Die Bildfigur ändert den Drehsinn, wenn \(\Delta<0\)

Umkehrabbildung

Um die Umkehrabbildung \(\alpha^{-1}\) zu bestimmen, vertauscht man \(x\) und \(y\) mit \(x'\) und \(y'\) und löst dann nach \(x'\) und \(y'\) auf. Oder allgemein:

\[\begin{align} x'&=\frac{1}{\Delta}(d\cdot x - b\cdot y)\\[11pt] y'&=\frac{1}{\Delta}(-c\cdot x + a\cdot y) \end{align}\]

Umkehrabbildungen existieren also nur dann, wenn \(\Delta\not=0\) gilt.

Verkettungen

Für Verkettungen \(\alpha\circ\beta\):

\[\alpha\circ\beta=\alpha(\beta(\vec{p}))\]

Spezielle Abbildungen

Drehung um den Origo

Drehung um den Origo

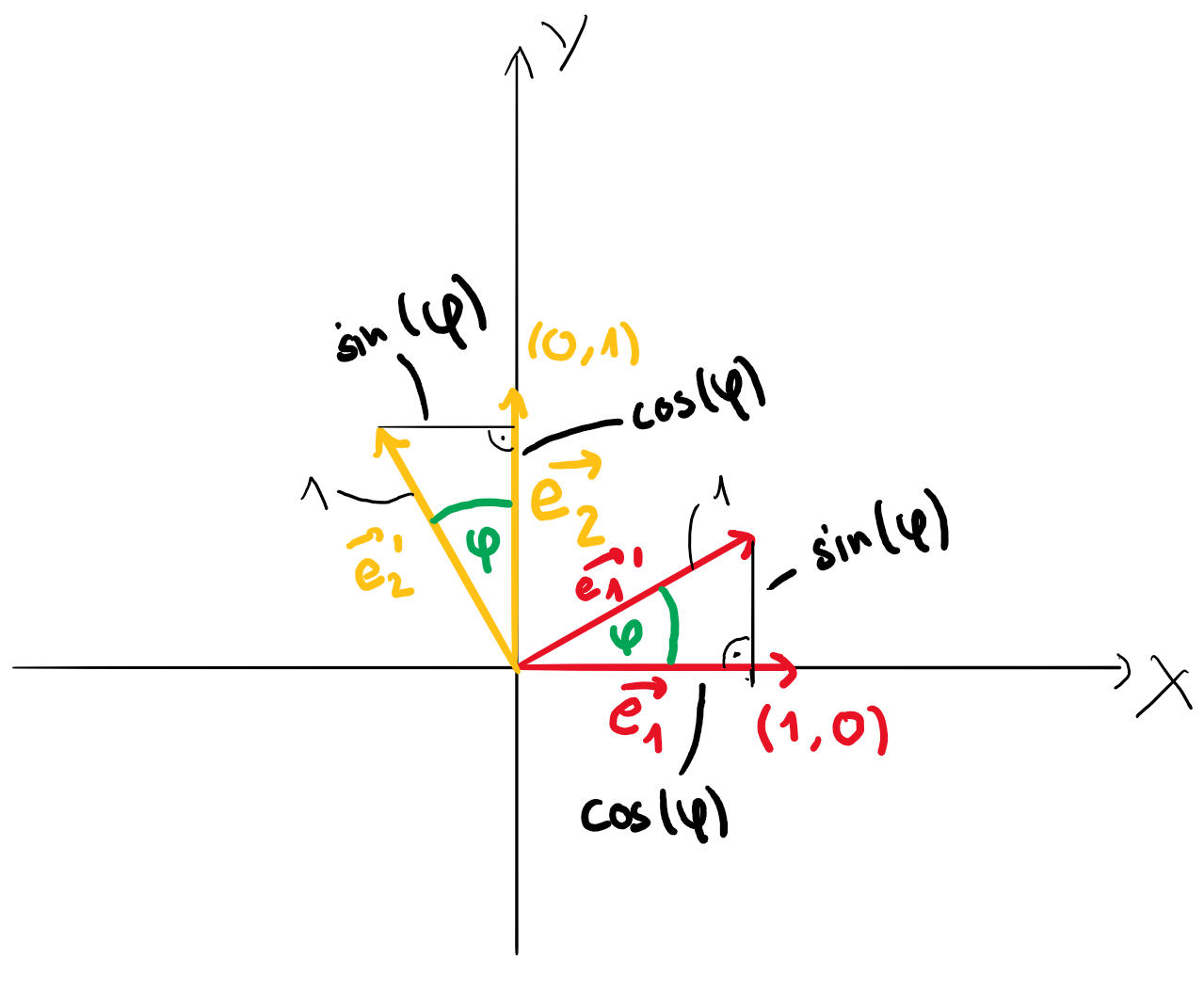
Für die Drehung mit Winkel \(\varphi\) um den Origo gilt:

\[\begin{align} x'&=\cos(\varphi)\cdot x - \sin(\varphi)\cdot y\\[11pt] y'&=\sin(\varphi)\cdot x + \cos(\varphi)\cdot y \end{align}\]

Spiegelung an einer Gerade

Spiegelung an einer Gerade

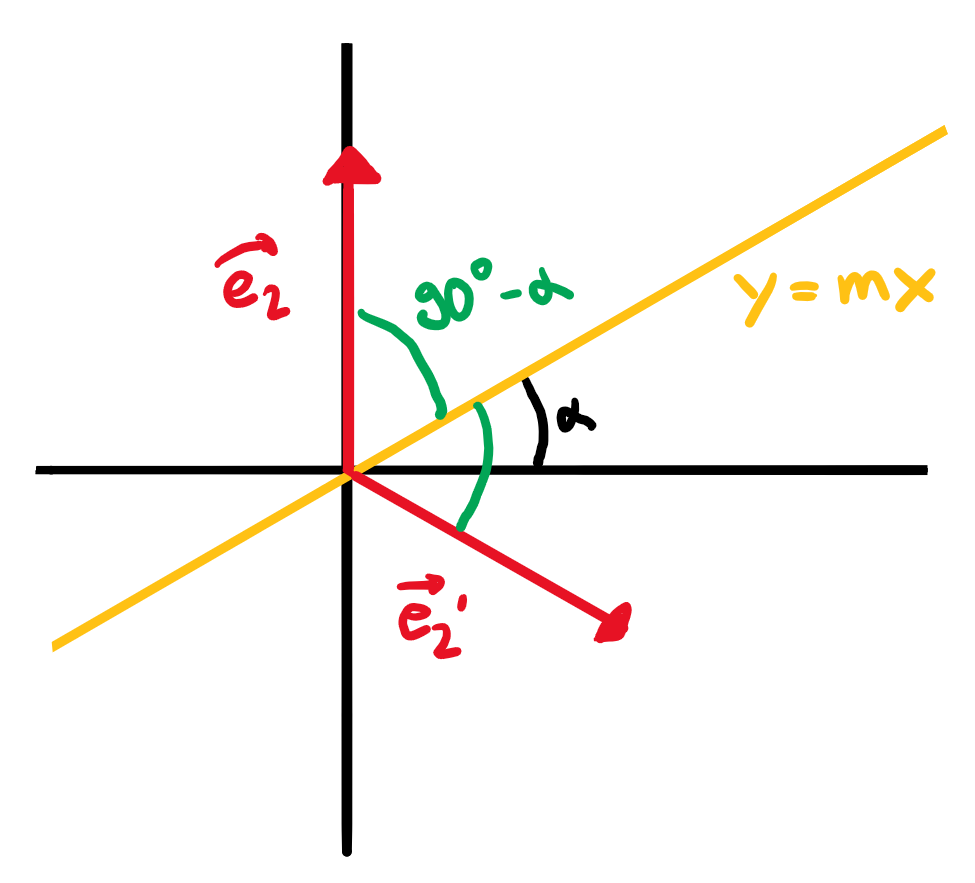
Für die Spiegelung an einer Gerade mit dem Neigungswinkel \(\alpha\) gilt:

\[\begin{align} x'&=\cos(2\alpha)\cdot x + \sin(2\alpha)\cdot y\\[11pt] y'&=\sin(2\alpha)\cdot x - \cos(2\alpha)\cdot y \end{align}\]

Gleichung von gedrehten Funktionen und Relationen

Wenn wir die Funktion \(f(x)\) (z. B. \(y=\frac{1}{2}x^2\)) um den Winkel \(\varphi\) drehen wollen (also die Relation \(r(x)\) gefunden werden soll), dann geht man wie folgt vor:

Man geht rückwärts von der Relation \(r(x)\) auf die Funktion \(f(x)\), weil die Funktionsgleichung schon gegeben ist:

\[\begin{align} x'&=\cos(-\varphi)\cdot x - \sin(-\varphi)\cdot y\\[11pt] y'&=\sin(-\varphi)\cdot x + \cos(-\varphi)\cdot y \end{align}\]

Jetzt ersetzt man \(x\) und \(y\) aus der Funktion (z. B. \(y=\frac{1}{2}x^2\)) mit den erhaltenen \(x'\) und \(y'\), z. B.:

\[(\sin(-\varphi)\cdot x + \cos(-\varphi)\cdot y )= \frac{1}{2}(\cos(-\varphi)\cdot x - \sin(-\varphi)\cdot y)^2\]
Last update: June 12, 2021