Integralrechnung I

Streifenmethode

Ausführliches Berechnen von Flächen unter Funktionen.

Vorbemerkung: Wichtige Formeln:

\[\sum_{k=1}^{n}k=\frac{n(n+1)}{2}\]
\[\sum_{k=1}^{n}k^2=\frac{n(n+1)(2n+1)}{6}\]
\[\sum_{k=1}^{n}k^3=\frac{n^2(n+1)^2}{4}\]

Grundidee

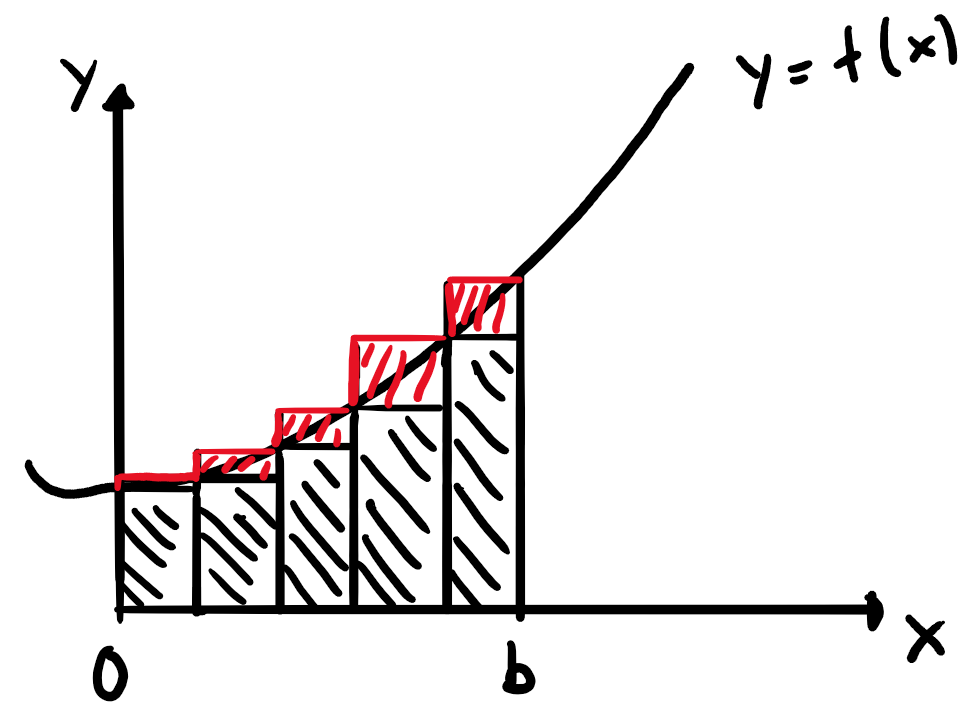
Streifenmethode

Die zu bestimmende Fläche (von z. B. 0 bis \(b\)) soll in \(n\) Streifen mit Breite \(\frac{b}{n}\), die einmal grösser (Obere Grenze mit Fläche \(O_n\)) und einmal kleiner (Untere Grenze mit Fläche \(U_n\)). Die tatsächliche Fläche \(A\) liegt dazwischen. Es gilt also \(U_n\leq A\leq O_n\). Wenn \(n\) zu \(\infty\) wächst, wird der Unterschied zwischen \(U_n\) und \(O_n\) immer kleiner, sodass \(A\) nun einen konkreten Wert bekommt: \(\lim_{n\to\infty}U_n=A=\lim_{n\to\infty}O_n\)

Alternativ kann man auch nur mit einer Grenze (z. B. \(O_n\)) und dann einfach \(A=\lim_{n\to\infty}O_n\) sagen:

\[\frac{b}{n}=\Delta x\]
\[O_n=\sum_{i=1}^{n}f(x_i)\Delta x\]
\[A=\lim_{n\to\infty}O_n\]

Beispiel

\(f(x)=\frac{1}{2}x^2-3x\)

\[\begin{align} O_n&=\sum_{i=1}^{n}\frac{b}{n}\left[\frac{1}{2}\left(\frac{i\cdot b}{n}\right)^2-3\left(\frac{i\cdot b}{n}\right)\right]\\[11pt] &=\frac{1}{2}\left(\frac{b}{n}\right)^3\left[\sum_{i=1}^{n}i^2\right]-3\left(\frac{b}{n}\right)^2\left[\sum_{i=1}^{n}i\right]\\[11pt] &=\frac{b^3n(n+1)(2n+1)}{12n^3}-\frac{3b^2n(n+1)}{2n^2}\\[11pt] &=\frac{b^3\cancel{n^3}(1+\frac{1}{n})(2+\frac{1}{n})}{12\cancel{n^3}}-\frac{3b^2\cancel{n^2}(1+\frac{1}{n})}{2\cancel{n^2}}\\[11pt] \lim_{n\to\infty}O_n&=\frac{1}{6}b^3-\frac{3}{2}b^2 \end{align}\]

Integralschreibweise

Für Flächen \(I(b)\) unter einem Abschnitt 0 bis \(b\) schreibt man:

\[I(b)=\int_{0}^{b}f(x)\,dx\]

Hauptsatz der Analysis

Beweis mit Differenzenquotienten \(\frac{\Delta I}{\Delta x}\) mit \(I(x)\) als Fläche / Integral (ähnlich zur Definition der Ableitung)

\[\begin{align} \Delta xf(x+\Delta x)&\leq\Delta I\leq\Delta xf(x)\\[11pt] f(x+\Delta x)&\leq\frac{\Delta I}{\Delta x}\leq f(x)\\[11pt] \lim_{\Delta x\to 0}f(x+\Delta x)&\leq\lim_{\Delta x\to 0}\frac{\Delta I}{\Delta x}\leq\lim_{\Delta x\to 0}f(x)\\[11pt] f(x)&\leq I'(x)\leq f(x) \end{align}\]

Die Integralfunktion \(I(x)\) abgeleitet gibt die Funktion \(f(x)\):

\[I'(x)=f(x)\]

Bestimmte Integrale

\(F(x)\) mit \(F'(x)=f(x)\) nennt man die Stammfunktion von \(f(x)\). Für bestimmte Integrale im Bereich von \(a\) bis \(b\) gilt:

\[\int_{a}^{b}f(x)\,dx=F(b)-F(a)\]

Theoretisch entsteht beim Integrieren immer noch eine Konstante \(C\), die allerdings bei bestimmten Integralen wegfällt bzw. sich selbst wegsubtrahiert.

Integralsätze

\[\int_{a}^{b}cf(x)\,dx=c\int_{a}^{b}f(x)\,dx\]
\[\int_{a}^{b}f(x)\,dx=-\int_{b}^{a}f(x)\,dx\]
\[\int_{a}^{b}f(x)\,dx=\int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\]
\[\int_{a}^{b}f(x)\pm g(x)\,dx=\int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]

Flächen bei Integralen

Integrale sind nur über der x-Achse tatsächliche Flächen. Darunter wird das Integral negativ und der Betrag muss genommen werden. Vor allem ist auf Nullstellen zwischen \(a\) und \(b\) zu achten. Dort müssen die Integrale zwischen den Nullstellen separat ausgerechnet werden.

Dieses Problem fällt weg, sobald die Fläche zwischen zwei Funktionen \(f(x)\) und \(g(x)\) berechnet werden muss. Idee dahinter ist die Verschiebung beider Funktionen um ein \(C\), welches sie im Raum von \(a\) und \(b\) oberhalb der x-Achse verschiebt. Dieses \(C\) fällt anschliessend weg und es gilt:

\[A=\int_{a}^{b}f(x)-g(x)\,dx\]

Selbst die Reihenfolge von \(f(x)\) und \(g(x)\) ist unwichtig.

Uneigentliche Integrale

Uneigentliche Integrale sind Integrale, bei denen unendlich lange Flächen mit je nachdem endlichen Flächeninhalt berechnet werden. Folgende Vorgehensweise wird verwendet:

\[\begin{align} \int_{a}^{\infty}f(x)\,dx&=\lim_{b\to\infty}\int_{a}^{b}f(x)\,dx\\[11pt] &=\lim_{b\to\infty}\left.F(x)\right|_a^b\\[11pt] &=\lim_{b\to\infty}F(b)-F(a) \end{align}\]

Rotationsvolumen V einer Funktion f(x)

Herleitung

Beweis mit Hilfe mit Zylinderscheiben statt den Streifen:

\[\begin{align} V&=\lim_{n\to\infty}\sum_{k=1}^{n}V_k\\[11pt] &=\lim_{n\to\infty}\sum_{k=1}^{n}\pi f^2(x)\Delta x\\[11pt] &=\int_a^b \pi f^2(x)\,dx\\[11pt] &=\pi \int_a^b f^2(x)\,dx \end{align}\]

Volumen V eines Torus ("Donut")

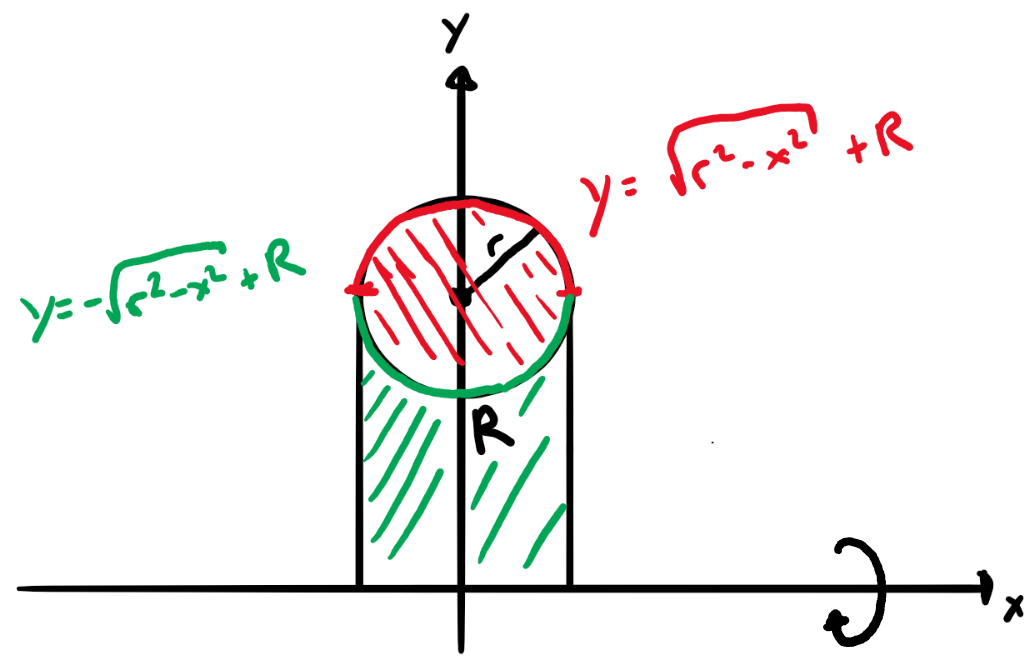
Donut

Ein Kreis mit Radius \(r\) und Abstand \(R\) zur x-Achse rotiert um diese.

\[\begin{align} V&=2\pi\int_0^r (\sqrt{r^2-x^2}+R)^2\,dx-2\pi\int_0^r (-\sqrt{r^2-x^2}+R)^2\,dx\\[11pt] &=2\pi\int_0^r (K+R)^2-(-K+R)^2\,dx\\[11pt] &=2\pi\int_0^r 4KR\,dx\\[11pt] &=8\pi R\int_0^r \sqrt{r^2-x^2}\,dx\\[11pt] &=2\pi^2r^2R \end{align}\]

Länge l einer Kurve

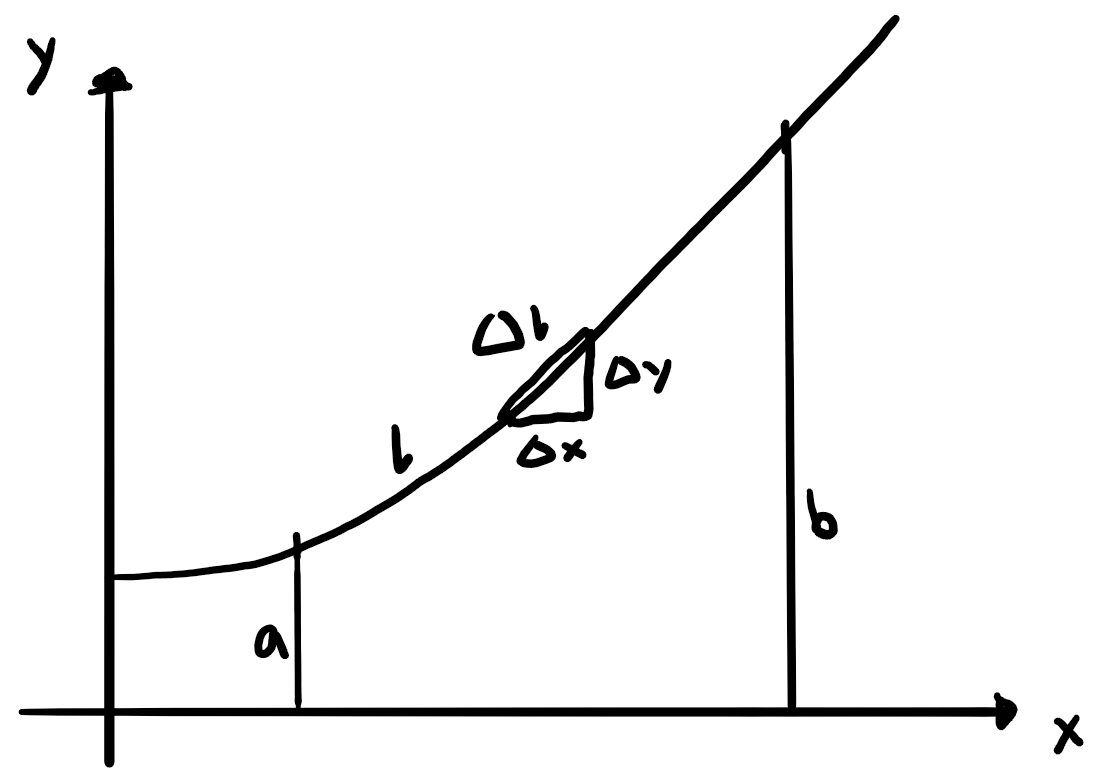
Idee mit \(n\) Dreiecken.

\[\begin{align} l&=\lim_{\Delta x\to 0}\sum_{i}\sqrt{\Delta x^2+\Delta y^2}\\[11pt] &=\lim_{\Delta x\to 0}\sum_{i}\sqrt{\Delta x^2\left(1+\left(\frac{\Delta y}{\Delta x}\right)^2\right)}\\[11pt] &=\lim_{\Delta x\to 0}\sum_{i}\sqrt{1+\left(\frac{\Delta y}{\Delta x}\right)^2}\Delta x\\[11pt] &=\int_a^b \sqrt{1+(y')^2}\,dx \end{align}\]

Mantelfläche M eines Rotationskörpers

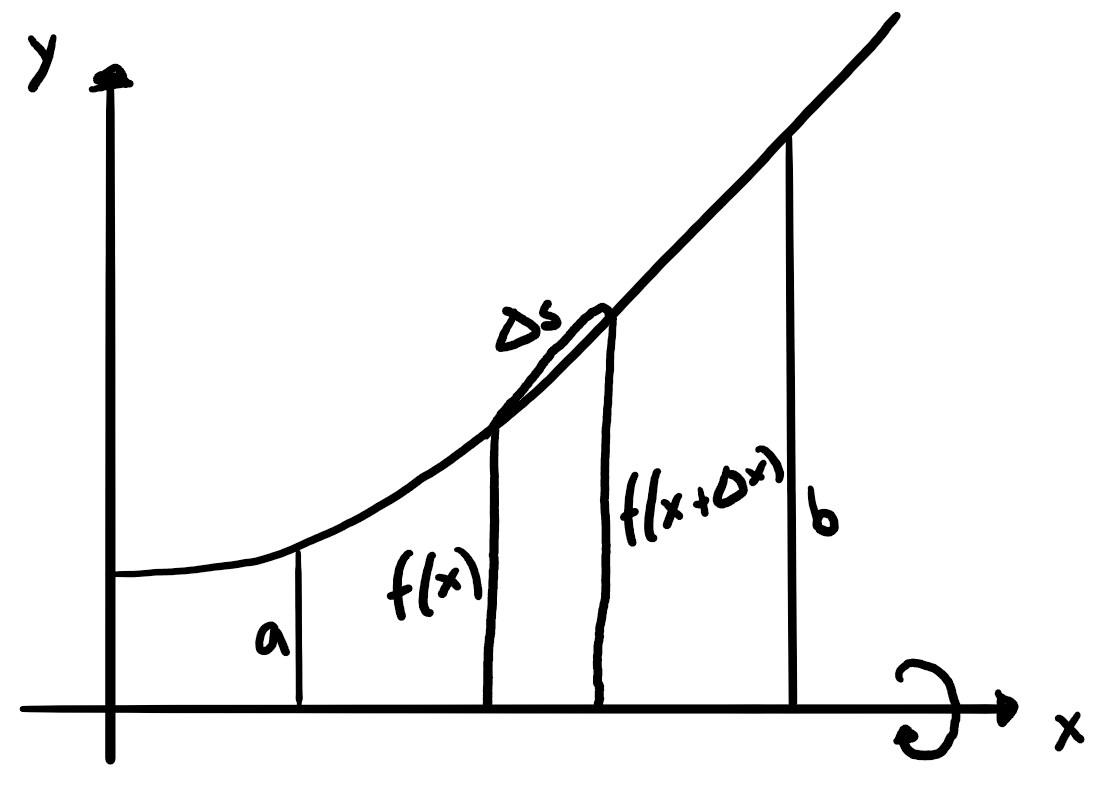
Idee mit Mantelfläche \(M=\pi(r_1+r_2)s\) der Zylinderscheiben mit Dicke \(s\):

\[\begin{align} M&=\lim_{\Delta x\to 0}\sum_i \pi(f(x)+f(x+\Delta x))\Delta s\\[11pt] &=\lim_{\Delta x\to 0}\pi\sum_i (f(x)+f(x+\Delta x))\sqrt{1+\left(\frac{\Delta y}{\Delta x}\right)^2}\Delta x\\[11pt] &=2\pi\int_a^b y\sqrt{1+(y')^2}\,dx \end{align}\]

Last update: June 7, 2021