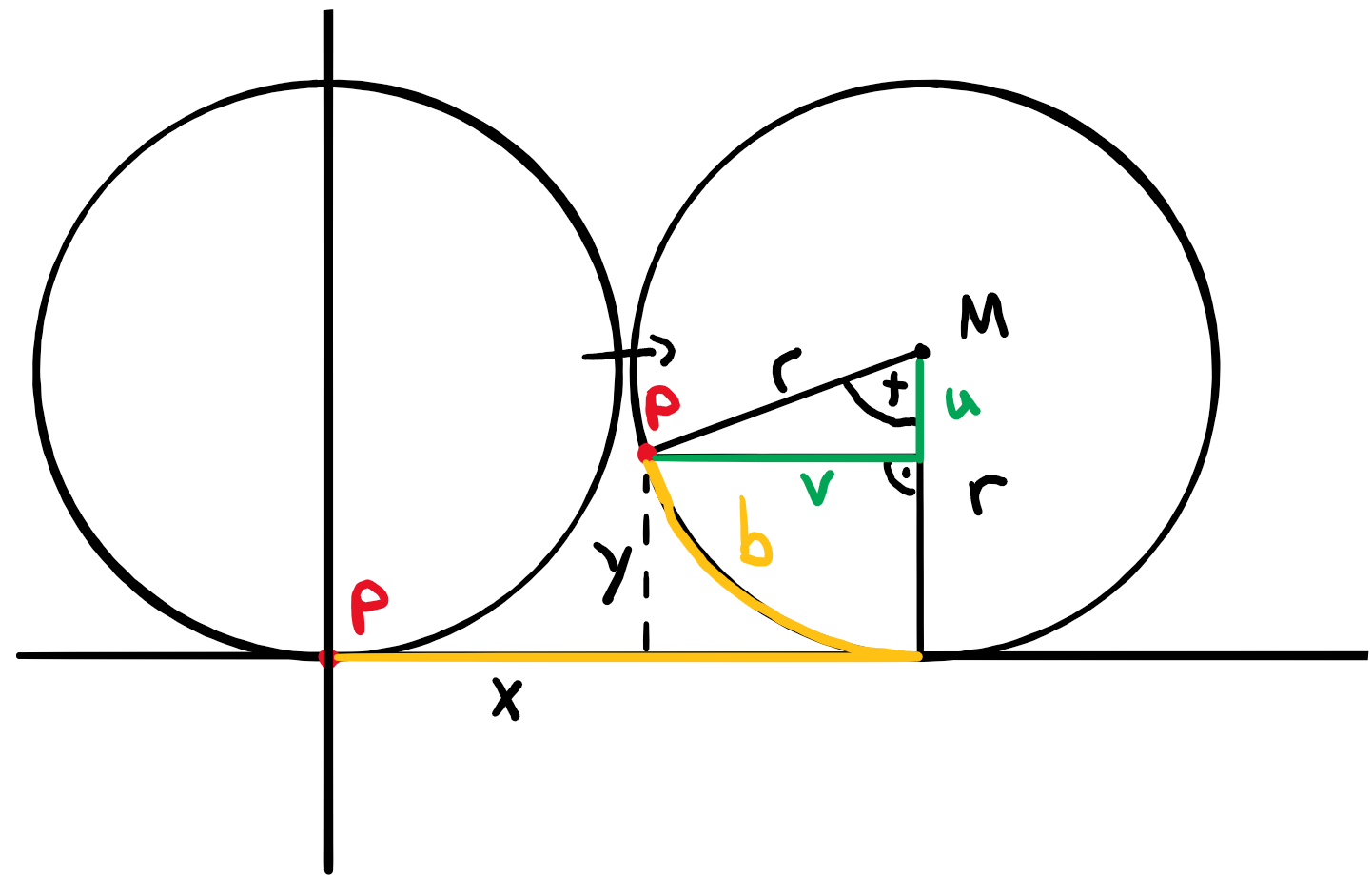Parameterfunktionen
Allgemein
Definition
Bei Parameterfunktionen werden die Koordinaten \(x\) und \(y\) mit Hilfe eines Parameters \(t\) definiert. Für einen Punkt \(P\) gilt also:
\[P(x(t)|y(t))\]
Kreise und Ellipsen
Ellipsen bzw. Kreise mit Hauptachse \(a\), Nebenachse \(b\) und Mittelpunkt \(M=(x_M|y_M)\) hat die Parameterfunktion:
\[\begin{align}
x(t)&=x_M+a\cdot\cos(t)\\[11pt]
y(t)&=y_M+b\cdot\sin(t)
\end{align}\]
Geschwindigkeit
Für die durchschnittliche Geschwindigkeit \(\bar{v}\) gilt:
\[\bar{v}=\begin{pmatrix}\frac{\Delta x}{\Delta t}\\\frac{\Delta y}{\Delta t}\end{pmatrix}=\frac{1}{\Delta t}\begin{pmatrix}\Delta x\\\Delta y\end{pmatrix}\]
Für die Momentangeschwindigkeit \(\vec{v}\) gilt:
\[\vec{v}=\lim_{\Delta t \to 0}\bar{v}=\begin{pmatrix}\dot x(t)\\\dot y(t)\end{pmatrix}\]
Steigung
Die Steigung der Tangente lässt sich wie folgt ableiten:
\[\begin{align}
y(t)&=f(x(t))\\[11pt]
\dot y(t)&=f'(x)\cdot\dot x(t)\\[11pt]
y'&=\frac{\dot y(t)}{\dot x(t)}
\end{align}\]
Für senkrechte und waagerechte Tangenten folgt:
\[\begin{align}
\dot y(t)&=0&&\textrm{Waagerechte Tangente}\\[11pt]
\dot x(t)&=0&&\textrm{Senkrechte Tangente}
\end{align}\]
Schräge Asymptoten
Auch für Asymptoten gilt:
\[y=m\cdot x+q\]
Wenn die Asymptote durch den Nullpunkt geht, dann gilt:
\[\begin{align}
m&=\frac{y}{x}\\[11pt]
&=lim_{t\to a}\frac{y(t)}{x(t)}\\[11pt]
\end{align}\]
Andernfalls werden \(m\) und \(q\) gegeben sein. Man zeigt dann, dass die Gleichung stimmt mit:
\[\lim_{t\to a}y(t)-m\cdot x(t)\stackrel{?}{=}q\]
Integrale
Für Integrale gilt:
\[\int_a^b f(x)\, dx=\int_{t_1}^{t_2} y(t)\dot x(t)\, dt\quad(\textrm{mit}\; x(t_1)=a,\,x(t_2)=b)\]
Bogenlänge
Für die Bogenlänge gilt:
\[\int_a^b \sqrt{1+y'^2}\, dx=\int_{t_1}^{t_2} \sqrt{\dot x(t)^2+\dot y(t)^2}\, dt\quad(\textrm{mit}\; x(t_1)=a,\,x(t_2)=b)\]
Beispiele
Zykloid
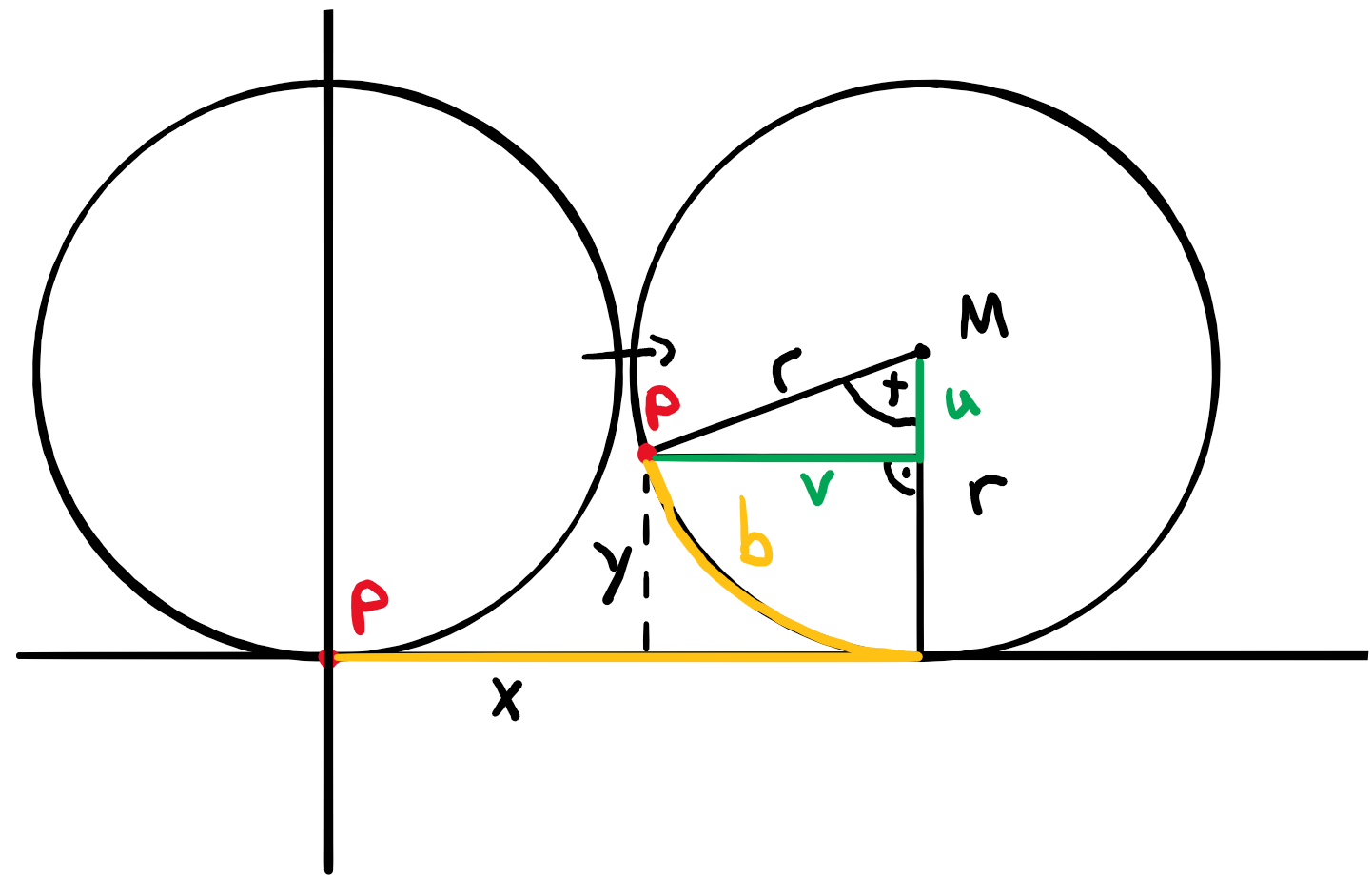
Es gilt:
\[\begin{align}
x(t)&=b-v=tr-v=tr-r\sin(t)=r(t-\sin(t))\\[11pt]
y(t)&=r-u=tr-v=r-r\cos(t)=r(1-\cos(t))
\end{align}\]
Parametrisierung des Einheitskreises
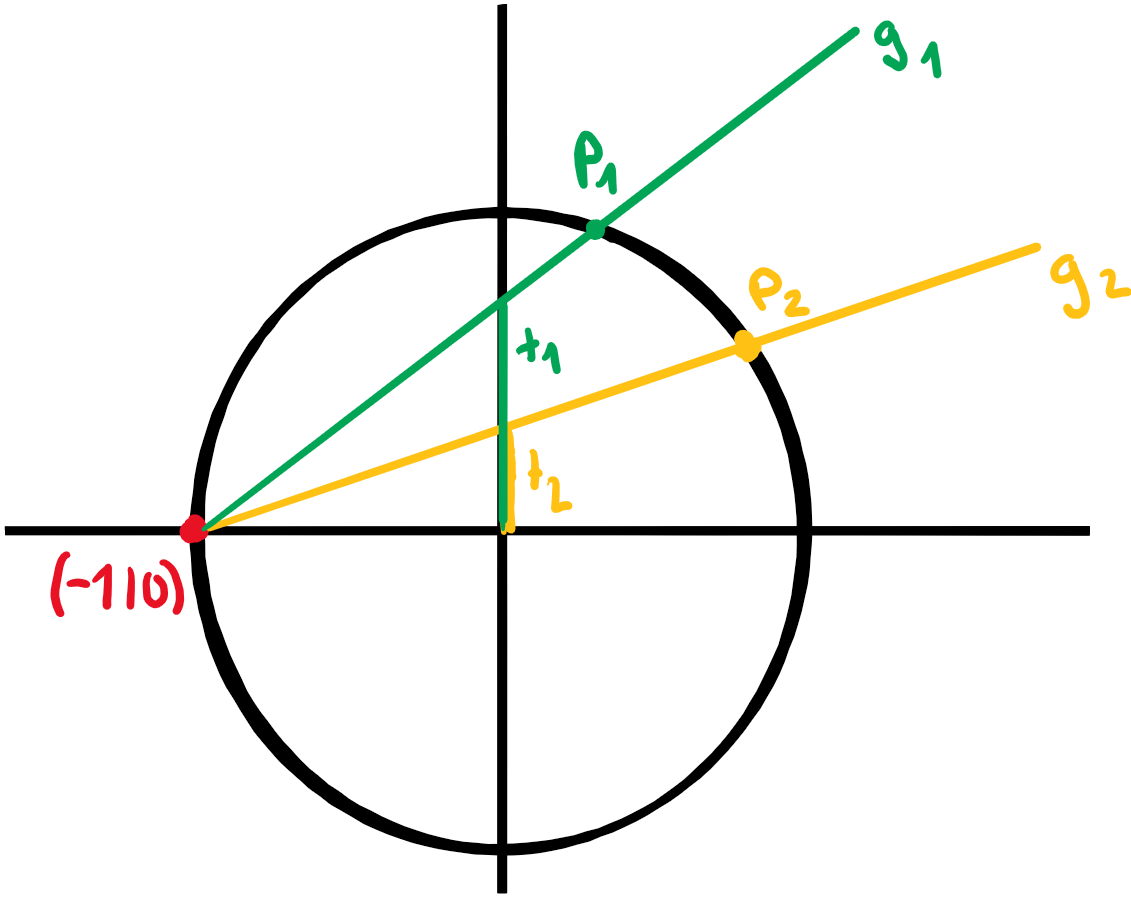
Für die Gerade gilt:
\[\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}-1\\0\end{pmatrix}+s\cdot \begin{pmatrix}1\\t\end{pmatrix}\]
Für den Einheitskreis gilt:
\[x^2+y^2=1\]
Setzt man beide zusammen gibt das:
\[\begin{align}
(-1+s)^2+(st)^2&=1\\[11pt]
s^2-2s+1+s^2t^2&=1\\[11pt]
s^2(t^2+1)-2s&=0\\[11pt]
s(s(1+t^2)-2)&=0\\[11pt]
s_1&=0\\[11pt]
s_2&=\frac{2}{1+t^2}
\end{align}\]
Wieder in die Gleichung der Gerade eingesetzt:
\[\begin{align}
x(t)&=\frac{2t}{1+t^2}\\[11pt]
y(t)&=\frac{1-t^2}{1+t^2}
\end{align}\]
Stab rutscht Wand hinunter
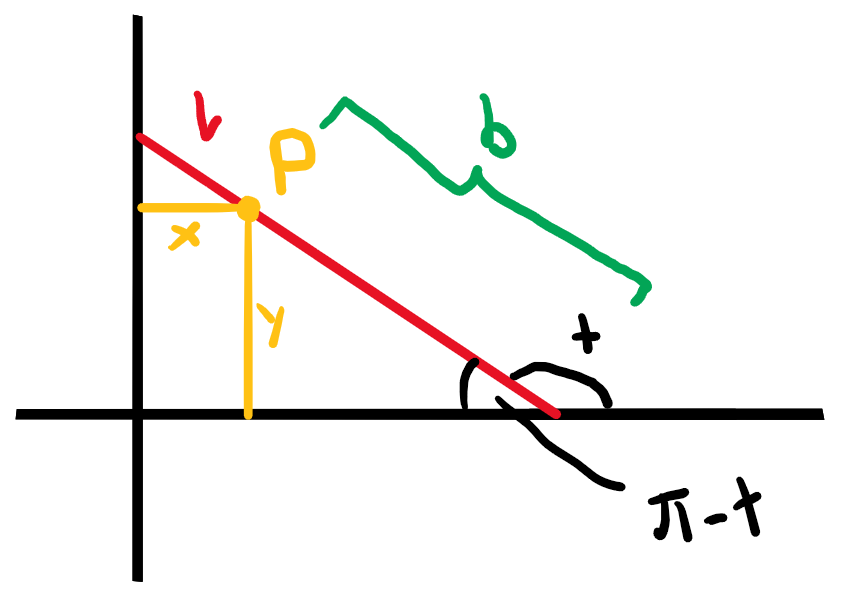
Es gilt:
\[\begin{align}
x(t)&=\cos(\pi - t)\cdot l-\cos(\pi-t)\cdot b=\cos(t)(b-l)\\[11pt]
y(t)&=\sin(\pi-t)\cdot b=\sin(t)\cdot b\\[11pt]
\end{align}\]
Als Ellipse (ohne \(t\)) aufgeschrieben:
\[\frac{x^2}{(b-l)^2}+\frac{y^2}{b^2}=1\]
Last update: June 15, 2021