Repetition Funktionen und Ergänzungen
Funktionen vs. Relationen
Funktionen sind eindeutige Zuordnungen aller \(x\in\mathbb{D}\) zu jeweiligen \(y\in\mathbb{W}\). Wenn dies sogar umgekehrt gilt, dann sind auch Umkehrfunktionen \(f^{-1}\) mit \(f^{-1}(f(x))=x\;\forall x\in\mathbb{D}\). Umkehrfunktionen können in diesem Fall mit Umtauschen von \(x\) und \(y\) erreicht werden.
Relationen sind bedingungslose Beziehungen zwischen \(y\) und \(x\). Beispiel hierfür sind Kreise und Ellipsen mit \((\frac{x}{a})^2+(\frac{y}{b})^2=1\).
Spezielle Punkte
x-Achse / Nullstelle
y-Achse
Schnittpunkte
Spezielle Funktionen
Geraden
Geraden haben eine Steigung \(m\) und einen y-Achsenabschnitt \(q\):
Parabeln
Quadratische Funktion
Quadratische Funktionen haben 2 typische Schreibweisen:
Erste Art
Zweite Art (mit (u|v) als Scheitelpunkt)
Weitere Parabeln / Hyperbeln
Funktionen mit \(y=x^k\) und \(k>1\) sind parabelförmig, wobei bei negativen \(k\) Hyperbeln entstehen. Bei beiden streben gerade \(k\) sowohl für negative als auch positive \(x\) zu \(\infty\). Bei ungeraden gehen die negativen Richtung \(-\infty\).
Symmetrien
Parabeln sind achsensymmetrisch (\(f(-x)=f(x)\forall x\)), wenn die Funktion nur gerade Exponenten besitzt, sie also wie folgt aufgeschrieben werden kann:
Parabeln sind punktsymmetrisch (\(f(-x)=-f(x)\forall x\)), wenn die Funktion nur ungerade Exponenten besitzt, sie also wie folgt aufgeschrieben werden kann:
Sinus / Cosinus / e / ln
Sowohl \(\sin\) als auch \(\cos\) besitzen \(\mathbb{D}=\mathbb{R}\) und \(\mathbb{W}=[-1;1]\) mit den jeweiligen Umkehrfunktionen \(\sin^{-1}=\arcsin\) und \(\cos^{-1}=\arccos\).
\(e^x\) hat \(\mathbb{D}=\mathbb{R}\) und \(\mathbb{W}=\mathbb{R}^+\). Die Umkehrfunktion ist der \(\ln\).
Funktionen bestimmen
Die einfachste Funktion die durch \(n\) Punkte gegeben ist, ist eine (\(n-1\))-ten Grades und kann also durch ein Gleichungssystem mit \(n\) Gleichungen bestimmt werden.
Stetigkeit / Differenzierbarkeit
Stetigkeit
Funktionen sind stetig, wenn ihr Graph ohne absetzen gezeichnet werden kann bzw.:
Differenzierbarkeit
Funktionen sind differenzierbar, wenn sie keinen Knick besitzen. Beispiel für nicht differenzierbare Funktionen wären \(y=|x^2-4|\) oder \(y=\begin{cases}-2x+1 &x<2\\ x+a &x\geq2\end{cases}\)
Neue Grenzwerte
\(\lim_{x\to 0}\frac{\sin(x)}{x}\) (Mit Hilfe der Fläche von Dreiecken und Kreissektoren)
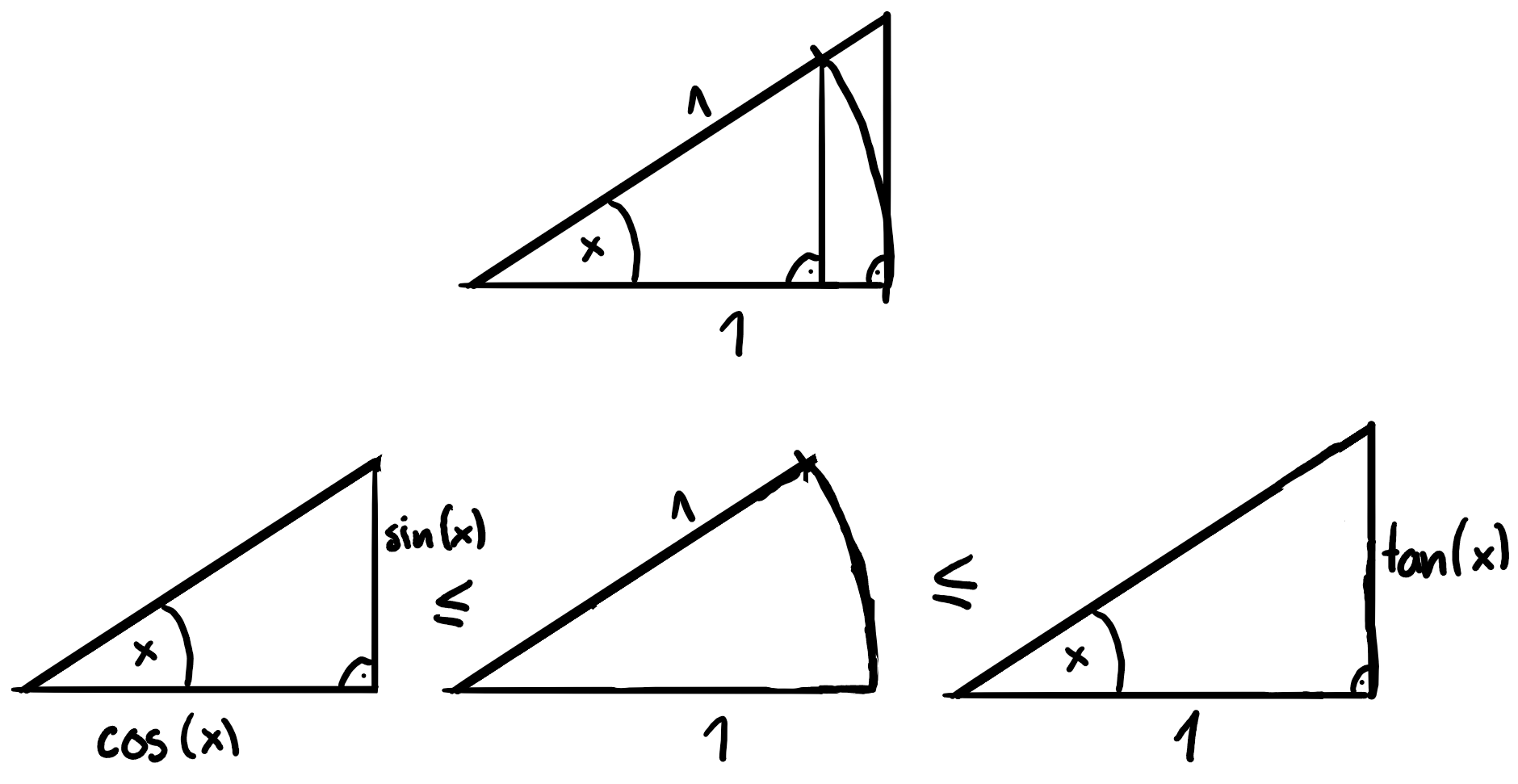
\(\lim_{x\to 0}\frac{\cos(x)-1}{x}\)
Alternativ mit De L'Hospital siehe Differentialrechnung II