Main

Wahrscheinlichkeitsrechnung

Bemerkung: Die meisten Aufgaben können auch mit Baumdiagrammen, statt klassischer Kombinatorik gelöst werden.

Begriffe / Schreibkonventionen

Ereignis

Ereignisse werden als \(E\) aufgeschrieben. Die Anzahl Elemente \(k\) in \(E\) sind \(|E|\).

Wahrscheinlichkeit

Wahrscheinlichkeit eines Ereignisses E: \(p(E)\)

Ergebnisraum

Alle möglichen Ergebnisse: \(\Omega\). Die Anzahl Elemente \(n\) in \(\Omega\) sind \(|\Omega|\)

Elementarereignisse

Einziges Element des Ergebnisraumes: \(\omega\)

Gegenereignis

Das Gegenereignis von \(E\) heisst \(\bar{E}\) ("E quer"). Es hat den Wert \(\bar{E}=1-E\)

Laplace-Wahrscheinlichkeit

Wenn alle Elementarereignisse \(\omega\) die gleiche Wahrscheinlichkeit haben, gilt:

\[p(E)=\frac{|E|}{|\Omega|}=\frac{k}{n}\]

Bedingte Wahrscheinlichkeiten

Allgemein

Ein Ergebnis kann unter einer bestimmten Bedingung auftauchen (Beim Baum hängt das unterste Ereignis von den oben angesetzten Bedingungen ab). Man schreibt für die Wahrscheinlichkeit: \(p(E|Bedingung)\) oder allgemein: \(p(A|B)\). Die Wahrscheinlichkeit, dass sowohl \(A\) als auch \(B\) eintreten wird \(p(A\wedge B)\) oder in der Mengenlehre \(A\cap B\) aufgeschrieben. Sie entspricht also der Multiplikation der Zahlen eines Astes beim Baum oder:

\[\begin{align} p(A\wedge B) &= p(A|B)\cdot p(B)\\[11pt] p(A|B)&=\frac{p(A\wedge B)}{p(B)} \end{align}\]

Für die umgekehrte Bedingung \(p(B|A)\) können wir (klarer mit Mengenlehre) Folgendes genau so gut schreiben:

\[p(B|A)=\frac{p(A\wedge B)}{p(A)} = \frac{p(A|B)\cdot p(B)}{p(A)}\]

Ereignisse gelten als unabhängig, wenn eines der Folgenden gilt:

1. \[p(A|B)=p(A)\]
2. \[p(A\wedge B)=p(A)\cdot p(B)\]
3. \[p(A|B)=p(A|\bar B)\]
4. \[p(\bar A\wedge B)=p(\bar A)\cdot p(\bar B)\]
5. ...

Umgekehrt sind \(A\) und \(B\) abhängig, wenn etwas nicht gilt.

Lösungsmethoden zu bedingten Wahrscheinlichkeiten

10% einer Bevölkerung sind krank. Ist man erkrankt, liefert der Diagnosetest zu 96% ein positives Testresultat; ist man gesund, liefert er zu 94% ein negatives Testresultat. Wie gross ist die Wahrscheinlichkeit, krank zu sein, wenn das Testresultat positiv ist?

\(\implies\) \(p(K)=0.1\), \(p(P|K)=0.96\), \(p(\bar P| \bar K)=0.94\)

\[p(K|P)=\text{?}\]

Baum und invertierter Baum

Mit diesen Informationen kann ein erster Wahrscheinlichkeiten-Baum aufgezeichnet werden:

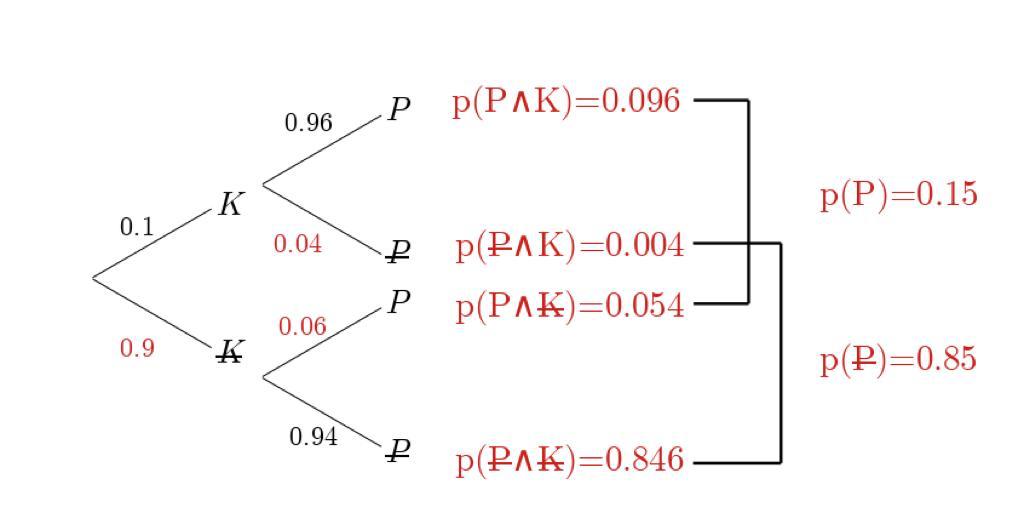
Das Gegenereignis errechnet sich durch die Formel \(p(\bar A)=1-p(A)\). Entlang eines Astes wird multipliziert, um die Wahrscheinlichkeit \(p(A\wedge B)\) zu erhalten.

Mit den farbigen Zahlen auf der rechten Seite kann nun ein umgedrehter Baum gezeichnet werden:

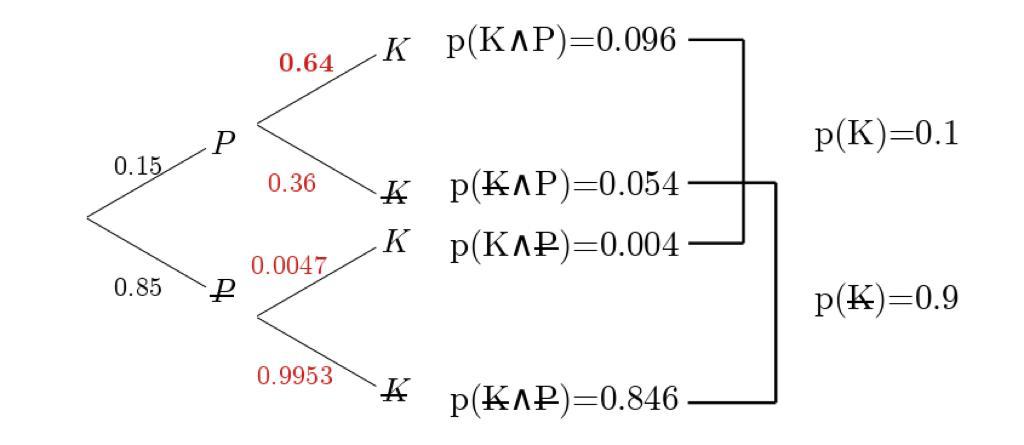
Die verbleibenden bedingten Wahrscheinlichkeiten werden berechnet durch \(p(B|A)=\frac{p(A\wedge B)}{p(B)}\). Es gilt \(p(A\wedge B)=p(B\wedge A)\). Also:

\[p(K|P)=\frac{p(K\wedge P)}{p(P)}=\frac{0.096}{0.15}=0.64=64~\% \]

Vier-Felder-Tafel

Einfacher geht die Berechnung mit einer Vier-Felder-Tafel. Sie hat folgende Struktur: Die erste Zeile und Spalte dienen der Namensgebung. Entlang der Zeilen und Spalten wird addiert.

	p( A )	p( \(\bar A\) )
p( B )	\(p(A\wedge B)\)	\(p(\bar A\wedge B)\)	\(p(B)\)
p( \(\bar B\) )	\(p(A\wedge \bar B)\)	\(p(\bar A\wedge \bar B)\)	\(p(\bar B)\)
	\(p(A)\)	\(p(\bar A)\)	1

Für die Beispielaufgabe sieht die Vier-Felder-Tafel wie folgt aus:

	p( P )	p( \(\bar P\) )
p( K )	\(0.96\times0.1=\) 0.096	0.1-0.096= 0.004	0.1
p( \(\bar K\) )	0.9-0.846 = 0.054	\(0.94\times 0.9=\) 0.846	0.9
	0.15	0.85	1

Mit \(p(B|A)=\frac{p(A\wedge B)}{p(B)}\) gilt also:

\[p(K|P)=\frac{p(K\wedge P)}{p(P)}=\frac{0.096}{0.15}=0.64=64~\% \]

Beispiel für unendliche Bäume

Jemand will sich mit 90% Wahrscheinlichkeit sicher sein, dass mindestens ein Tier einen Gendefekt aufweist, der bei 5% der Tiere auftritt. Wie viele Tiere \(n\) braucht er?

Die Wahrscheinlichkeit, dass kein Tier einen Defekt aufweist ist \(p(\bar{E}) = 0.95^n\). D. h.:

\[\begin{align} p(E)= 1 - 0.95^n&\geq 0.9\\[11pt] 0.1&\geq 0.95^n\\[11pt] n&\geq 44.89\rightarrow 45 \end{align}\]

Oder allgemein:

\[n = \log_{p(\textrm{kein Deffekt})}(1-p(\textrm{mind. Sicherheit}))\]

Primzahlsatz

Abschätzung für \(\frac{1}{1}+\frac{1}{2}+..+\frac{1}{n}\):

\[\begin{align} \int_{1}^{n}\frac{1}{x}\,dx+\frac{1}{n}&<\frac{1}{1}+\frac{1}{2}+..+\frac{1}{n}\\[11pt] \ln(n)+\frac{1}{n}&<\frac{1}{1}+\frac{1}{2}+..+\frac{1}{n}\\[11pt] \ln(n)&\approx\frac{1}{1}+\frac{1}{2}+..+\frac{1}{n} \end{align}\]

Abschätzung für \(\prod_{p\leq x}(1-\frac{1}{p})\) wobei \(p\) prim ist:

\[\begin{align} \prod_{p\leq x}\left(1-\frac{1}{p}\right)^{-1}&=\left(1-\frac{1}{2}\right)^{-1}\left(1-\frac{1}{3}\right)^{-1}\left(1-\frac{1}{5}\right)^{-1}...\left(1-\frac{1}{p}\right)^{-1}\\[11pt] &\Downarrow\;\left(\textrm{mit}\,s=\frac{a_1}{1-q}\right)\\[11pt] &=\left(1+\frac{1}{2}+\frac{1}{4}+...\right)\left(1+\frac{1}{3}+\frac{1}{9}+...\right)\left(1+\frac{1}{5}+\frac{1}{25}+...\right)...\left(1+\frac{1}{p}+\frac{1}{p^2}+...\right)\\[11pt] &=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+...+\frac{1}{p}+...+\frac{1}{x}...\textrm{Rest}\\[11pt] \prod_{p\leq x}\left(1-\frac{1}{p}\right)&\approx\frac{1}{\frac{1}{1}+\frac{1}{2}+...+\frac{1}{x}} \end{align}\]

Beweis für die Anzahl Primzahlen kleiner/gleich \(x\) oder \(\pi(x)\) mit der Wahrscheinlichkeit p(x), dass eine Zahl zwischen 1 und \(x\) prim ist:

\[\begin{align} p(x)&=\frac{\pi(x)}{x}\\[11pt] \pi(x)&=xp(x)\\[11pt] &\approx x\left[\left(1-\frac{1}{2}\right)\left(1-\frac{1}{3}\right)\left(1-\frac{1}{5}\right)...\left(1-\frac{1}{p}\right)\right]\\[11pt] &\approx x\left[\frac{1}{\frac{1}{1}+\frac{1}{2}+...+\frac{1}{x}}\right] \approx x\left[\frac{1}{\ln(x)}\right]\\[11pt] p(x)&\approx\frac{x}{\ln(x)} \end{align}\]

---

Last update: June 6, 2021